
����Ŀ����DZͧ��Ϊ����λһ�����˴�������е�һ�֣�����һ��������˵����ˮ�º��������Ҫս������.�ҹ��ĺ�DZͧ��չѸ�٣���γ�ɫ�����ս��Ѳ������.һ�Σ�ij�ͺź�DZͧ��ˮ��400��![]() ����600��/���ӵ��ٶ�������������ʱ������б�Ϸ�����Ϊ
����600��/���ӵ��ٶ�������������ʱ������б�Ϸ�����Ϊ![]() ˮ����
ˮ����![]() ����һ���ɴ�ֻ��������ͬ�����У�����2���Ӻ�
����һ���ɴ�ֻ��������ͬ�����У�����2���Ӻ�![]() �����ٴβ�ÿ��ɴ�ֻ������Ϊ
�����ٴβ�ÿ��ɴ�ֻ������Ϊ![]() ��
��![]() �����������������������ɴ�ֻ���е��ٶ�.���ο����ݣ�
�����������������������ɴ�ֻ���е��ٶ�.���ο����ݣ�![]() ��
��![]() ��
��![]() ��
��![]() ��
��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ÿ���˶�Ӧ���ж�ˮ�ľ�η֮�ģ��ӵ�����𣬽�ˮ����ˮ����������������������磮ij�ؽ����������ɺ���Ϊ������Լ��ˮ���õز����ˡ�����ˮ�ۡ��Ʒѷ��������巽����ÿ��ÿ����ˮ��������4�ֵ�ÿ��2Ԫ������4�ֶ�������6�ֵģ�����4�ֵIJ���ÿ��4Ԫ������6�ֵģ�����6�ֵIJ���ÿ��6Ԫ���õ�һ��ͥ��¼��ȥ��12���µ�����ˮ�����±������й�����ˮ����ͳ�������ᷢ���ı���ǣ�������
��ˮ��x���֣� | 3 | 4 | 5 | 6 | 7 |
Ƶ�� | 1 | 2 | 5 | 4��x | x |
A. ƽ��������λ�� B. ��������λ�� C. ƽ���������� D. ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����C����ABΪֱ������O�ϣ�BD�����C�����ߴ�ֱ�ڵ�D��BD����O���ڵ�E��
��1����֤��BCƽ�֡�DBA��
��2������AE��AC����cos��ABD��![]() ��OA��m����д�����ı���AEDC�����˼·��
��OA��m����д�����ı���AEDC�����˼·��
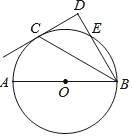
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
�У�![]() �ֱ����������ϣ�
�ֱ����������ϣ�![]() ��
��![]() ,
,![]() ,
,![]() ��
��
��1��д��ͼ�е����������Σ���֤����
��2����![]() ��
��![]() ʱ����
ʱ����![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ADBC�ڽ�����O��ABΪ��O��ֱ�����Խ���AB��CD�ཻ�ڵ�E��
��1����֤����BCD+��ABD��90�㣻
��2����G��AC���ӳ����ϣ�����BG������O�ڵ�Q��CA��CB����ABD����ABG����GH��CD����DC���ӳ����ڵ�H����֤��GQ��![]() GH��
GH��
��3���ڣ�2���������£�����B��BF��AD����CD�ڵ�F��GH��3CH����CF��4![]() ������O�İ뾶��
������O�İ뾶��
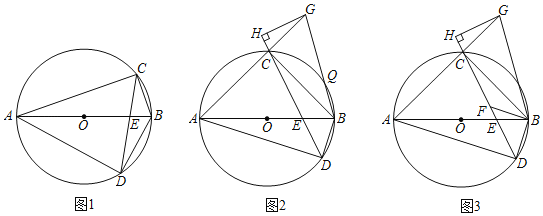
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��ֱ��l������A����2��0���͵�B��0��1������M��x���ϣ�����M��x��Ĵ��߽�ֱ��l�ڵ�C����OM��2OA������C�ķ�������������ʽΪ��������
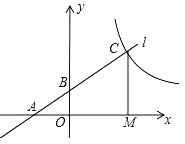
A.y��![]() B.y��
B.y��![]() C.y��
C.y��![]() D.y��
D.y��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���蹤��һ�������д�����ɳʯ��Ҫ���䣮���蹫˾������������Ϊ8�ֺ�10�ֵĿ�����14����ȫ������һ��������128��ɳʯ��
��1�����蹫˾����������Ϊ8�ֺ�10�ֵĿ������ж�������
��2�����Ź��̵Ľ�չ��������Ҫһ������ɳʯ����190�֣�Ϊ����������������������ֿ�����7������������¹���������Ϊ8�ֵĿ�����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���л�������ԴԶ�������л����֣�Ԣ�����.Ϊ�����л����㴫ͳ�Ļ���ij��ѧ��������֯��һ��ȫУ2000��ѧ���μӵ���������д������.Ϊ�˽Ȿ�δ����ijɼ���ѧУ�����������ȡ������200��ѧ���ijɼ���Ϊ��������ͳ�ƣ��Ƴ����²�������ͳ��ͼ����
�ɼ�x���֣������� | Ƶ�����ˣ� | Ƶ�� |
50��x<60 | 10 | 0.05 |
60��x<70 | 30 | 0.15 |
70��x<80 | 40 | 0.2 |
80��x<90 | m | 0.35 |
90��x<100 | 50 | n |
Ƶ���ֲ�ֱ��ͼ
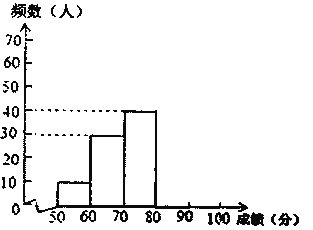
������������Ϣ���ش��������⣺
��1��m=________��n=________��
��2����ȫƵ���ֲ�ֱ��ͼ��
��3����200��ѧ���ɼ�����λ��������________�����Σ�
��4�����ɼ���90�����ϣ�����90�֣�Ϊ�������ȣ�������Ƹ�У�μӱ��α�����2000��ѧ���гɼ����������ȵ�Լ�ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
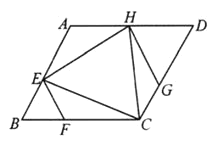
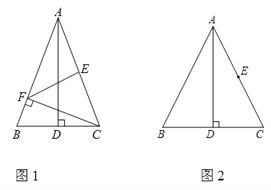
����Ŀ������ǡ�ABC�У�AB=AC��ADΪBC���ϵĸߣ�EΪAC�е㣮
��1����ͼ1������C��CF��AB��F�㣬����EF������BAD=20�㣬���AFE�Ķ�����
��2����MΪ�߶�BD�ϵĶ��㣨��M���D���غϣ�������C��CN��AM��N�㣬����EN��AB����P�㣮
�������⽫ͼ2��ȫ��
��С��ͨ���۲졢ʵ�飬������룺�ڵ�M�˶��Ĺ����У�ʼ���С�APE=2��MAD��
С������������ͬѧ�ǽ������ۣ��γ���֤���ò���ļ����뷨��
�뷨1������DE��Ҫ֤��APE=2��MAD��ֻ��֤��PED=2��MAD��
�뷨2�����MAD=������DAC=����ֻ������������ʾ����PEC��ͨ���Ƕȼ���á�APE=2����
�뷨3����NE��ȡ��Q��ʹ��NAQ=2��MAD��Ҫ֤��APE=2��MAD��ֻ��֤��NAQ�ס�APQ������
����ο�������뷨������С��֤����APE =2��MAD����һ�ַ������ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com