
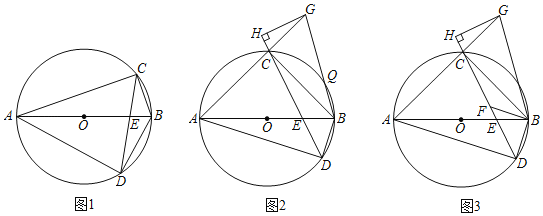
【题目】如图,四边形ADBC内接于⊙O,AB为⊙O的直径,对角线AB、CD相交于点E.
(1)求证:∠BCD+∠ABD=90°;
(2)点G在AC的延长线上,连接BG,交⊙O于点Q,CA=CB,∠ABD=∠ABG,作GH⊥CD,交DC的延长线于点H,求证:GQ=![]() GH.
GH.
(3)在(2)的条件下,过点B作BF∥AD,交CD于点F,GH=3CH,若CF=4![]() ,求⊙O的半径.
,求⊙O的半径.
【答案】(1)见解析;(2)见解析;(3)⊙O的半径为2![]() .
.
【解析】
(1)由圆周角定理可得∠ACB=90°=∠ADB,即可得结论;
(2)过点A作AM⊥AD,交DC的延长线于点M,连接AQ,MG,通过证明△AMG≌△AQG,可得MG=GQ,∠AMG=∠AQG=90°,可证HM=HG,即可得结论;
(3)延长MG与DB的交点为N,延长BF交AG于点P,通过证明△PCF∽△GCM,可得MC=CF=![]() ,MG=PF,通过证明△HGC∽△DAB,可得AD=3BD,由MD=
,MG=PF,通过证明△HGC∽△DAB,可得AD=3BD,由MD=![]() AD,可求BD的长,即可求⊙O的半径.
AD,可求BD的长,即可求⊙O的半径.
证明:(1)∵AB是直径,
∴∠ACB=90°=∠ADB,
∴∠ACD+∠BCD=90°,
∵∠ACD=∠ABD,
∴∠BCD+∠ABD=90°;
(2)如图,过点A作AM⊥AD,交DC的延长线于点M,连接AQ,MG.

∵AB是直径
∴∠AQB=∠ACB=∠ADB=90°
∵CA=CB
∴∠ABC=∠BAC=45°
∴∠ADC=∠ABC=45°
∵AM⊥AD
∴∠ADM=∠AMD=45°
∴AM=AD,
∵∠ABD=∠ABG,∠AQB=∠ADB,AB=AB
∴△AQB≌△ADB(AAS)
∴AD=AQ,∠BAD=∠BAQ
∴AQ=AM,
∵∠CAB=45°
∴∠BAD+∠MAG=45°,∠BAQ+∠GAQ=45°
∴∠MAG=∠GAQ,且AM=AD,AG=AG
∴△AMG≌△AQG(SAS)
∴MG=GQ,∠AMG=∠AQG=90°
∵∠AMD=45°
∴∠GMH=45°
∵GH⊥MD
∴∠HMG=∠HGN=45°
∴HM=HG
∴MG=![]() HG
HG
∴GQ=![]() HG;
HG;
(3)如图,延长MG与DB的交点为N,延长BF交AG于点P.

∵∠MAD=∠AMN=∠ADB=90°
∴四边形ADNM是矩形,且AD=AM
∴四边形ADNM是正方形
∴AM=AD=MN=DN,MN∥AD
∴∠GAD=∠AGM=∠AGB
∵BF∥AD
∴∠GPB=∠GAD=∠AGB
∴BG=BP,且BC⊥AG
∴PC=CG
∵BP∥AD∥MN
∴△PCF∽△GCM
∴![]() =1
=1
∴MC=CF=![]() ,MG=PF,
,MG=PF,
∵∠ACD=∠HCG=∠ABD,∠GHC=∠ADB=90°
∴△HGC∽△DAB
∴![]() ,且GH=3CH,
,且GH=3CH,
∴AD=3BD
∵∠CDB=∠CAB=45°,∠FBD=90°
∴FD=![]() BD
BD
∵AD=AM,∠MAD=90°
∴MD=![]() AD
AD
∴![]() +
+![]() +
+![]() BD=
BD=![]() ×3BD
×3BD
∴BD=4
∴AD=12
∴AB=![]() =
=![]()
∴⊙O的半径为![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
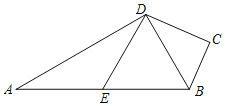
(1)求证:BD平分∠ABC;
(2)连接EC,若∠A=30°,DC=![]() ,求EC的长.
,求EC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为5的正方形ABCD中,点E,F分别是BC,DC边上的两个动点(不与点B,C,D重合),且AE⊥EF.
(1)如图1,当BE=2时,求FC的长;
(2)延长EF交正方形ABCD外角平分线CP于点P.
①依题意将图2补全;
②小京通过观察、实验提出猜想:在点E运动的过程中,始终有AE=PE.小京把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的三种想法:
想法1:在AB上截取AG=EC,连接EG,要证AE=PE,需证△AGE≌△ECP.
想法2:作点A关于BC的对称点H,连接BH,CH,EH.要证AE=PE,需证△EHP为等腰三角形.
想法3:将线段BE绕点B顺时针旋转90°,得到线段BM,连接CM,EM,要证AE=PE,需证四边形MCPE为平行四边形.
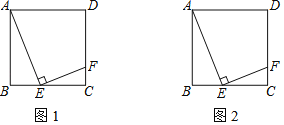
请你参考上面的想法,帮助小京证明AE=PE.(一种方法即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】核潜艇作为“三位一体”核打击力量中的一种,对于一个国家来说,是水下核威慑的重要战略武器.我国的核潜艇发展迅速,多次出色完成了战略巡航任务.一次,某型号核潜艇在水下400米的![]() 处以600米/分钟的速度向正东方向航行时,发现斜上方仰角为
处以600米/分钟的速度向正东方向航行时,发现斜上方仰角为![]() 水面上
水面上![]() 处有一可疑船只正沿着相同航向航行,跟踪2分钟后到达
处有一可疑船只正沿着相同航向航行,跟踪2分钟后到达![]() 处,再次测得可疑船只在仰角为
处,再次测得可疑船只在仰角为![]() 的
的![]() 处,请根据以上条件求出可疑船只航行的速度.(参考数据:
处,请根据以上条件求出可疑船只航行的速度.(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
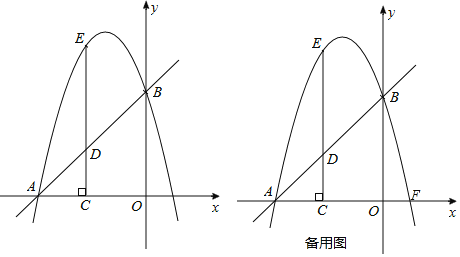
【题目】如图,已知抛物线![]() 与x轴负半轴相交于点A,与y轴正半轴相交于点B,
与x轴负半轴相交于点A,与y轴正半轴相交于点B,![]() ,直线l过A、B两点,点D为线段AB上一动点,过点D作
,直线l过A、B两点,点D为线段AB上一动点,过点D作![]() 轴于点C,交抛物线于点E.
轴于点C,交抛物线于点E.
(1)求抛物线的解析式;
(2)若抛物线与x轴正半轴交于点F,设点D的横坐标为x,四边形FAEB的面积为S,请写出S与x的函数关系式,并判断S是否存在最大值,如果存在,求出这个最大值;并写出此时点E的坐标;如果不存在,请说明理由.
(3)连接BE,是否存在点D,使得![]() 和
和![]() 相似?若存在,求出点D的坐标;若不存在,说明理由.
相似?若存在,求出点D的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是矩形ABCD的边CD上一点,把△ADE沿AE对折,使点D恰好落在BC边上的F点处.已知折痕AE=10![]() ,且CE:CF=4:3,那么该矩形的周长为( )
,且CE:CF=4:3,那么该矩形的周长为( )
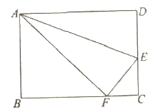
A.48B.64C.92D.96
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让市民享受到更多的优惠,某市针对乘坐地铁的人群进行了调查.
(1)为获得乘坐地铁人群的月均花费信息,下列调查方式中比较合理的是 ;
A.对某小区的住户进行问卷调查
B.对某班的全体同学进行问卷调查
C.在市里的不同地铁站,对进出地铁的人进行问卷调查
(2)调查小组随机调查了该市1000人上一年乘坐地铁的月均花费(单位:元),绘制了频数分布直方图,如图所示.

① 根据图中信息,估计平均每人乘坐地铁的月均花费的范围是 元;
A.20—60 B.60—120 C.120—180
②为了让市民享受到更多的优惠,相关部门拟确定一个折扣线,计划使30%左右的人获得折扣优惠.根据图中信息,乘坐地铁的月均花费达到 元的人可以享受折扣.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com