
【题目】如图,已知△ABC的面积为24,点D在线段AC上,点F在线段BC的延长线上,且BF=4CF,四边形DCFE是平行四边形,则图中阴影部分的面积为( )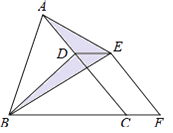
A.3
B.4
C.6
D.8
【答案】A
【解析】连接EC,过A作AM∥BC交FE的延长线于M,
∵四边形CDEF是平行四边形,
∴DE∥CF,EF∥CD,
∴AM∥DE∥CF,AC∥FM,
∴四边形ACFM是平行四边形,
∵△BDE边DE上的高和△CDE的边DE上的高相同,
∴△BDE的面积和△CDE的面积相等,
同理△ADE的面积和△AME的面积相等,
即阴影部分的面积等于平行四边形ACFM的面积的一半,是 ![]() ×
× ![]() CF×hCF ,
CF×hCF ,
∵△ABC的面积是24,BC=4CF
∴ ![]() BC×hBC=
BC×hBC= ![]() ×4CF×hCF=24,
×4CF×hCF=24,
∴CF×hCF=12,
∴阴影部分的面积是 ![]() ×
× ![]() ×12=3,
×12=3,
故答案为:A.
连接EC,过A作AM∥BC交FE的延长线于M,根据已知易证四边形ACFM是平行四边形,根据同底等高的两个三角形的面积相等,得出△BDE的面积和△CDE的面积相等,△ADE的面积和△AME的面积相等,从而证得阴影部分的面积等于平行四边形ACFM的面积的一半,就可求出CF×hCF的值,即可得出答案。


 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣2x2+8x﹣6与x轴交于点A、B,把抛物线在x轴及其上方的部分记作C1,将C1向右平移得C2,C2与x轴交于点B,D.若直线y=x+m与C1、C2共有3个不同的交点,则m的取值范围是____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用直尺画图(先用铅笔画图,然后再用墨水笔将符合条件的图形画出).
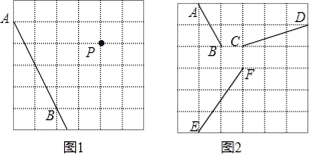
(1)利用图1中的网格,过P点画直线AB的平行线和垂线;
(2)平移图(2)网格中的三条线段AB、CD、EF,使平移后三条线段首尾顺次相接组成一个三角形;
(3)如果每个方格的边长是单位1,那么图(2)中组成的三角形的面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】统计显示,2013年底杭州市各类高中在校学生人数大约是11.4万人,将11.4万用科学记数法表示应为( )
A.11.4×102
B.1.14×103
C.1.14×104
D.1.14×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了抓住市文化艺术节的商机,某商店决定购进A,B两种艺术节纪念品.若购进A种纪念品8件,B种纪念品3件,需要950元;若购进A种纪念品5件,
B种纪念品6件,需要800元.
(1)求购进A,B两种纪念品每件各需多少元?
(2)若该商店决定购进这两种纪念品共100件,考虑市场需求和资金周转,用于购买这100件纪念品的资金不少于7500元,但不超过7650元,那么该商店共有几种进货方案?
(3)若销售每件A种纪念品可获利润20元,每件B种纪念品可获利润30元,在(2)问的各种进货方案中,哪一种方案获利最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)经过点A(﹣3,0)、B(1,0)、C(﹣2,1),交y轴于点M.
(1)求抛物线的表达式;
(2)D为抛物线在第二象限部分上的一点,作DE垂直x轴于点E,交线段AM于点F,求线段DF长度的最大值,并求此时点D的坐标;
(3)抛物线上是否存在一点P,作PN垂直x轴于点N,使得以点P、A、N为顶点的三角形与△MAO相似(不包括全等)?若存在,求点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个四边形的周长是48厘米,已知第二边长比第一边长的2倍多3厘米,第三边长等于第一边长和第二边长的和,第四边长与第一边长相等.则这个四边形第二边长是( )
A.6厘米B.15厘米C.16厘米D.21厘米
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com