
分析 根据形如-2,-1,0,1,2是整数;无限循环小数或有限小数是有理数;无限不循环小数是无理数;小于零的实数是负实数,可得答案.
解答 解:整数:{ 0,$\sqrt{(-5)^{2}}$,$\root{3}{-125}$…};
有理数:{ 1$\frac{2}{3}$,$\sqrt{0.25}$,0.$\stackrel{•}{3}$,0,$\sqrt{(-5)^{2}}$,$\frac{5}{11}$,$\root{3}{-125}$…};
无理数:{ $\sqrt{8}$,-3.030030003…,π…};
负实数:{-3.030030003…,$\root{3}{-125}$…};
故答案为:0,$\sqrt{(-5)^{2}}$,$\root{3}{-125}$;1$\frac{2}{3}$,$\sqrt{0.25}$,0.$\stackrel{•}{3}$,0,$\sqrt{(-5)^{2}}$,$\frac{5}{11}$,$\root{3}{-125}$;$\sqrt{8}$,-3.030030003…,π;-3.030030003…,$\root{3}{-125}$.
点评 本题考查了实数,无限循环小数或有限小数是有理数;无限不循环小数是无理数;有理数和无理数统称实数.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 在平行四边形ABCD中,过点A作两邻边CB,CD的垂线段AP,AQ,连接PQ,作AM⊥PQ于点M,作PN⊥AQ于点N,AM,PN交于点K,AC中点为点O,当点K,O,Q在同一条直线上时,若PQ=3.5,AC=4,则AK的长度为$\frac{\sqrt{15}}{2}$.
在平行四边形ABCD中,过点A作两邻边CB,CD的垂线段AP,AQ,连接PQ,作AM⊥PQ于点M,作PN⊥AQ于点N,AM,PN交于点K,AC中点为点O,当点K,O,Q在同一条直线上时,若PQ=3.5,AC=4,则AK的长度为$\frac{\sqrt{15}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
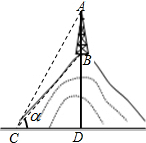 如图,在铅直高度为200m的小山上建有一座电视转播塔,某数学兴趣小组为测量电视转播塔的高度,在山脚的C处测得山顶B的仰角为30°(即∠BCD=30°),测得塔顶的仰角为45°(即∠ACD=45°),请根据以上数据求塔高AB.(精确到1m.备用数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).
如图,在铅直高度为200m的小山上建有一座电视转播塔,某数学兴趣小组为测量电视转播塔的高度,在山脚的C处测得山顶B的仰角为30°(即∠BCD=30°),测得塔顶的仰角为45°(即∠ACD=45°),请根据以上数据求塔高AB.(精确到1m.备用数据:$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.732).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com