
 (1)已知x2-x-3=0,求$\frac{{x}^{2}-1}{{x}^{3}+{x}^{2}}$÷(x-$\frac{2x-1}{x}$)的值.
(1)已知x2-x-3=0,求$\frac{{x}^{2}-1}{{x}^{3}+{x}^{2}}$÷(x-$\frac{2x-1}{x}$)的值.分析 (1)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把已知等式变形后代入计算即可求出值;
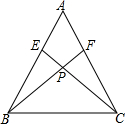
(2)利用SAS得到三角形ACE与三角形ABF全等,利用全等三角形对应角相等得到一对角相等,再由AB=AC,利用等边对等边得到两个底角相等,利用等式性质得到∠PBC=∠PCB,利用等角对等边即可得证.
解答 解:(1)原式=$\frac{(x+1)(x-1)}{{x}^{2}(x+1)}$÷$\frac{{x}^{2}-2x+1}{x}$=$\frac{x-1}{{x}^{2}}$•$\frac{x}{(x-1)^{2}}$=$\frac{1}{{x}^{2}-x}$,
由x2-x-3=0,得到x2-x=3,
则原式=$\frac{1}{3}$;
(2)在△AEC和△AFB中,
$\left\{\begin{array}{l}{AC=AB}\\{∠A=∠A}\\{AE=AF}\end{array}\right.$,
∴△AEC≌△AFB(SAS),
∴∠ABF=∠ACE,
∵AB=AC,
∴∠ABC=∠ACB,
∴∠PBC=∠PCB,
则PB=PC.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:填空题
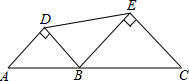 如图,A、B、C三点在同一直线上,以AB、BC为斜边分别作等腰直角三角形ABD和BCE,连接DE.若AC=4,则DE的取值范围是2≤DE$<2\sqrt{2}$.
如图,A、B、C三点在同一直线上,以AB、BC为斜边分别作等腰直角三角形ABD和BCE,连接DE.若AC=4,则DE的取值范围是2≤DE$<2\sqrt{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 要调查人们对“低碳生活”的了解程度,宜采用普查方式 | |
| B. | 一组数据3,4,4,6,8,5的众数和中位数都是3 | |
| C. | 必然事件的概率是100%,随机事件的概率是50% | |
| D. | 甲组数据的方差S甲2=0.13,乙组数据的方差S乙2=0.04;则乙组数据比甲组数据稳定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 11×104千米/时 | B. | 1.1×104千米/时 | C. | 1.1×105千米/时 | D. | 1.1×106千米/时 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| 0.5以下 | 0.7 | 0.8 | 0.9 | 1.0 | 1.0以上 |
| 5% | 8% | 5% | 40% | 30% | 12% |
| A. | 40% | B. | 1.0 | C. | 0.9 | D. | 5% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{4}{9}$ | C. | $\frac{17}{36}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
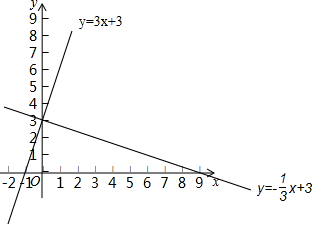 如图,在平面直角坐标系中,直线y=3x+3与x轴交于B点,与y轴交于A点,直线y=-$\frac{1}{3}$x+3与x轴交于C点,同时也过A点,请判断;两直线有怎样的位置关系?并说明理由.
如图,在平面直角坐标系中,直线y=3x+3与x轴交于B点,与y轴交于A点,直线y=-$\frac{1}{3}$x+3与x轴交于C点,同时也过A点,请判断;两直线有怎样的位置关系?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com