
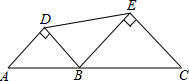
 如图,A、B、C三点在同一直线上,以AB、BC为斜边分别作等腰直角三角形ABD和BCE,连接DE.若AC=4,则DE的取值范围是2≤DE$<2\sqrt{2}$.
如图,A、B、C三点在同一直线上,以AB、BC为斜边分别作等腰直角三角形ABD和BCE,连接DE.若AC=4,则DE的取值范围是2≤DE$<2\sqrt{2}$. 分析 设AB=x,则BC=4-x,然后分别表示出DC、EC,继而在RT△DCE中,利用勾股定理求出DE长度的表达式,利用函数的知识进行解答即可.
解答 解:如图,连接DE.设AB=x,则BC=4-x,
∵△ACD和△BCE分别是等腰直角三角形,
∴∠DCA=45°,∠ECB=45°,DC=$\frac{\sqrt{2}}{2}x$,CE=$\frac{\sqrt{2}}{2}$(4-x),
∴∠DCE=90°,DB=$\frac{\sqrt{2}}{2}$x,$\frac{\sqrt{2}}{2}$(4-x)
故DE2=DC2+CE2=$\frac{1}{2}$x2+$\frac{1}{2}$(4-x)2=x2-4x+8=(x-2)2+4,
当x=2时,DE2取得最小值,DE也取得最小值,最小值为2,
DE<DB+BE=$\frac{\sqrt{2}}{2}$x+$\frac{\sqrt{2}}{2}$(4-x)=2$\sqrt{2}$
所以DE的取值范围是2≤DE<2$\sqrt{2}$.
点评 此题考查了二次函数最值及等腰直角三角形,难度不大,关键是表示出DC、CE,得出DE的表达式,还要求我们掌握配方法求二次函数最值.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
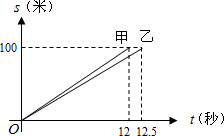 假定甲乙两人在一次赛跑中,路程S(米)与时间t(秒)的关系式如图所示,那么可以知道:
假定甲乙两人在一次赛跑中,路程S(米)与时间t(秒)的关系式如图所示,那么可以知道:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
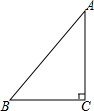 在Rt△ABC中,AB=10cm,BC=6cm,AC=8cm,问以点C为圆心,r为半径的⊙C与直线AB有怎样的位置关系:
在Rt△ABC中,AB=10cm,BC=6cm,AC=8cm,问以点C为圆心,r为半径的⊙C与直线AB有怎样的位置关系:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
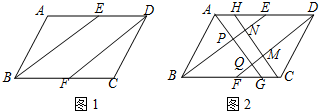
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
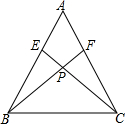 (1)已知x2-x-3=0,求$\frac{{x}^{2}-1}{{x}^{3}+{x}^{2}}$÷(x-$\frac{2x-1}{x}$)的值.
(1)已知x2-x-3=0,求$\frac{{x}^{2}-1}{{x}^{3}+{x}^{2}}$÷(x-$\frac{2x-1}{x}$)的值.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com