
| A. | $\frac{5}{12}$ | B. | $\frac{4}{9}$ | C. | $\frac{17}{36}$ | D. | $\frac{1}{2}$ |
分析 由二次函数y=x2+mx+n的图象与x轴没有公共点,可得△<0,即m2-4n<0,然后根据题意列出表格,由表格求得所有等可能与二次函数y=x2+mx+n的图象与x轴没有公共点的情况,再利用概率公式即可求得答案.
解答 解:∵二次函数y=x2+mx+n的图象与x轴没有公共点,
∴△<0,即m2-4n<0,
∴m2<4n,
列表得:
| 6 | (1,6) | (2,6) | (3,6) | (4,6) | (5,6) | (6,6) |
| 5 | (1,5) | (2,5) | (3,5) | (4,5) | (5,5) | (6,5) |
| 4 | (1,4) | (2,4) | (3,4) | (4,4) | (5,4) | (6,4) |
| 3 | (1,3) | (2,3) | (3,3) | (4,3) | (5,3) | (6,3) |
| 2 | (1,2) | (2,2) | (3,2) | (4,2) | (5,2) | (6,2) |
| 1 | (1,1) | (2,1) | (3,1) | (4,1) | (5,1) | (6,1) |
| 1 | 2 | 3 | 4 | 5 | 6 |
点评 此题考查了列表法或树状图法求概率.用到的知识点为:概率=所求情况数与总情况数之比.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
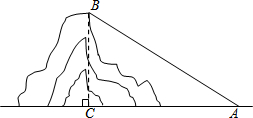 如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为32°,缆车速度为每分钟50米,从山脚下A到达山顶B缆车需要16分钟,求山的高度BC.(精确到0.1米)
如图,在莲花山滑雪场滑雪,需从山脚下乘缆车上山,缆车索道与水平线所成的角为32°,缆车速度为每分钟50米,从山脚下A到达山顶B缆车需要16分钟,求山的高度BC.(精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)已知x2-x-3=0,求$\frac{{x}^{2}-1}{{x}^{3}+{x}^{2}}$÷(x-$\frac{2x-1}{x}$)的值.
(1)已知x2-x-3=0,求$\frac{{x}^{2}-1}{{x}^{3}+{x}^{2}}$÷(x-$\frac{2x-1}{x}$)的值.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
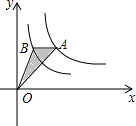 如图,点A和点B在第一象限,A是双曲线y=$\frac{3}{x}$上的一点,B是双曲线y=$\frac{1}{x}$上的一点,且AB平行于x轴,连接OA,OB,则△AOB的面积为1.
如图,点A和点B在第一象限,A是双曲线y=$\frac{3}{x}$上的一点,B是双曲线y=$\frac{1}{x}$上的一点,且AB平行于x轴,连接OA,OB,则△AOB的面积为1.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
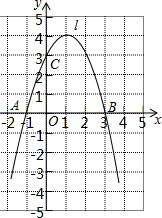 已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.
已知抛物线y=ax2+bx+c经过A(-1,0)、B(3,0)、C(0,3)三点,直线l是抛物线的对称轴.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
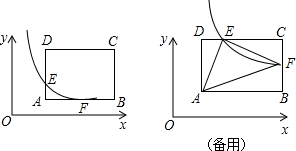
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
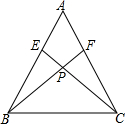
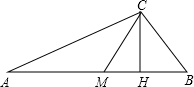 如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )
如图,已知△ABC中,∠ACB=90°,CH、CM分别是斜边AB上的高和中线,则下列结论不正确的是( )| A. | AB2=AC2+BC2 | B. | CH2=AH•HB | C. | CM=$\frac{1}{2}$AB | D. | CB=$\frac{1}{2}$AB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com