
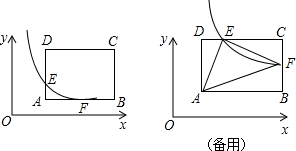
分析 (1)根据矩形性质,点与坐标的关系,由A、C坐标得B、D坐标;
(2)利用数形结合,根据反比例函数解析式,过点A,C时求出k的值,从而确定k的取值范围;
(3)根据反比例函数图象的性质,表示出E、F的坐标,用矩形ABCD的面积减去△CEF,△ADE,△ABF的面积,即可表示出△AEF的面积,根据点D、C的坐标即可得到k的取值范围;
(4)利用勾股定理,即可得到k的值;
(5)根据k的取值范围,得EF的最大值.
解答 解:(1)由点与坐标的关系可得:
B(6,1),D(2,4);
(2)当双曲线y=$\frac{k}{x}$过A(2,1)时,k=2,
当双曲线y=$\frac{k}{x}$过C(6,4)时,k=24,
∴2≤k≤24;
(3)当E,F分别在DC和BC上时,曲线y=$\frac{k}{x}$与CD,BC相交,
当y=4时,x=$\frac{k}{4}$,∴E($\frac{k}{4}$,4),CE=6-$\frac{k}{4}$
当x=6时,y=$\frac{k}{6}$,∴F(6,$\frac{k}{6}$),CF=4-$\frac{k}{6}$,
DE=$\frac{k}{4}$-2,AD=4-1=3,BF=$\frac{k}{6}$-1,AB=6-2=4,
y=(4-1)(6-2)-$\frac{1}{2}$($\frac{k}{4}$-2)×(4-1)-$\frac{1}{2}×$(6-2)×($\frac{k}{6}$-1)-$\frac{1}{2}$(6-$\frac{k}{4}$)(4-$\frac{k}{6}$)=-$\frac{1}{48}$k2+$\frac{7}{24}$k+5,
∴y与k之间的函数关系式为:y=-$\frac{1}{48}$k2+$\frac{7}{24}$k+5;
∴8≤k<24;
(4)当8≤k<24时,
曲线y=$\frac{k}{x}$与CD,BC相交,
${AF}^{2}{=AB}^{2}{+BF}^{2}=16{+(\frac{k}{6}-1)}^{2}$=$\frac{{k}^{2}}{36}-\frac{k}{3}+17$,
AE2=AD2+DE2=$\frac{{k}^{2}}{16}-k+13$,
EF2=CE2+CF2=${\frac{13}{144}k}^{2}-\frac{13}{3}k+52$
当AF2=AE2+EF2时,
解得:k=16或k=24(舍去),
当AE2=AF2+EF2时,
无解,
∴当k=16时,△AEF是直角三角形;
(5)由(4)知${EF}^{2}=\frac{13}{144}$k2$-\frac{13}{3}k$+52,
当EF2最大时,EF最大,
∵8≤k<24,由二次函数的性质可得:
当k=8时,EF2最大为:$\frac{13}{144}$×82-$\frac{13}{3}×8$+52=$\frac{208}{9}$
∴EF的最大值为$\frac{4\sqrt{13}}{3}$.
点评 本题主要考查了反比例函数的图象性质,勾股定理,矩形性质,利用数形结合思想是解决本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 4个 | B. | 3个 | C. | 2个 | D. | 1个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 11×104千米/时 | B. | 1.1×104千米/时 | C. | 1.1×105千米/时 | D. | 1.1×106千米/时 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{5}{12}$ | B. | $\frac{4}{9}$ | C. | $\frac{17}{36}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
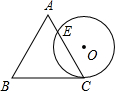 如图,一个边长为a的等边三角形ABC的高与⊙O的直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则AE:EC的值为( )
如图,一个边长为a的等边三角形ABC的高与⊙O的直径相等,⊙O与BC相切于点C,⊙O与AC相交于点E,则AE:EC的值为( )| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
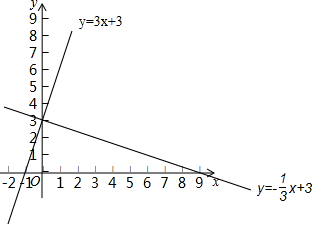 如图,在平面直角坐标系中,直线y=3x+3与x轴交于B点,与y轴交于A点,直线y=-$\frac{1}{3}$x+3与x轴交于C点,同时也过A点,请判断;两直线有怎样的位置关系?并说明理由.
如图,在平面直角坐标系中,直线y=3x+3与x轴交于B点,与y轴交于A点,直线y=-$\frac{1}{3}$x+3与x轴交于C点,同时也过A点,请判断;两直线有怎样的位置关系?并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com