
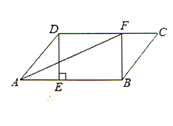
【题目】在□ABCD中,过点D作DE⊥AB于点E,点F在CD上,CF=AE,连接BF,AF.
(1)求证:四边形BFDE是矩形;
(2)若AF平分∠BAD,且AE=3,DE=4,求矩形BFDE的面积.
【答案】(1)四边形BFDE是矩形,见解析;(2)20.
【解析】
(1)首先证明四边形BFDE是平行四边形,再根据有一个角是90°的平行四边形是矩形即可判定;
(2)首先证明AD=DF,然后运用勾股定理求出AD的长即可解决问题.
解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,即BE∥DF,
∵CF=AE,
∴DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形.
(2)因为AB∥CD ,
所以∠BAF=∠AFD,
因为AF平分∠BAD,
所以∠DAF=∠AFD,
所以AD=DF,
在直角三角形ADE中,
因为AE=3,DE=4,
所以AD=![]() =5,
=5,
所以矩形的面积=4×5=20.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:
【题目】某校为了了解本校九年级学生的视力情况(视力情况分为:不近视,轻度近视,中度近视,重度近视),随机对九年级的部分学生进行了抽样调查,将调查结果进行整理后,绘制了如下不完整的统计图,其中不近视与重度近视人数的和是中度近视人数的2倍.

请你根据以上信息解答下列问题:
(1)求本次调查的学生人数;
(2)补全条形统计图,在扇形统计图中,“不近视”对应扇形的圆心角度数是 144 度;
(3)若该校九年级学生有1050人,请你估计该校九年级近视(包括轻度近视,中度近视,重度近视)的学生大约有多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
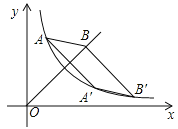
【题目】如图,已知反比例函数![]() 与正比例函数
与正比例函数![]() 的图象,点
的图象,点![]() ,点
,点![]() 与点
与点![]() 均在反比例函数的图象上,点
均在反比例函数的图象上,点![]() 在直线
在直线![]() 上,四边形
上,四边形![]() 是平行四边形,则
是平行四边形,则![]() 点的坐标为__________.
点的坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
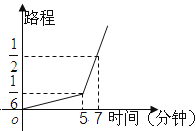
【题目】一名考生步行前往考场,5分钟走了总路程的![]() ,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1,出租车匀速),则他到达考场所花的时间比一直步行提前了________分钟。
,估计步行不能准时到达,于是他改乘出租车赶往考场,他的行程与时间关系如图所示(假定总路程为1,出租车匀速),则他到达考场所花的时间比一直步行提前了________分钟。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,格点三角形![]() (顶点为网格线的交点)的顶点
(顶点为网格线的交点)的顶点![]() ,
,![]() 的坐标分别为
的坐标分别为![]() ,
,![]() .
.

(1)请在网格图中建立平面直角坐标系;
(2)将![]() 先向左平移5个单位长度,再向下平移6个单位长度,请画出两次平移后的
先向左平移5个单位长度,再向下平移6个单位长度,请画出两次平移后的![]() ,并直接写出点
,并直接写出点![]() 的对应点
的对应点![]() 的坐标;
的坐标;
(3)若![]() 是
是![]() 内一点,直接写出
内一点,直接写出![]() 中的对应点
中的对应点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
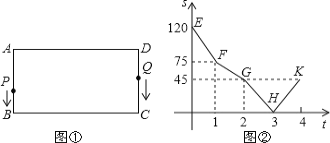
【题目】如图①,在矩形ABCD中,AB=30cm,BC=60cm.点P从点A出发,沿A→B→C→D路线向点D匀速运动,到达点D后停止;点Q从点D出发,沿D→C→B→A路线向点A匀速运动,到达点A后停止。若点P、Q同时出发,在运动过程中,Q点停留了1s,图②是P、Q两点在折线AB→BC→CD上相距的路程S(cm)与时间t(s)之间的函数关系图象。
(1)请解释图中点H的实际意义?
(2)求P、Q两点的运动速度;
(3)当时间t为何值时,△PCQ为等腰三角形?请直接写出t的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,2分别是某款篮球架的实物图与示意图,已知底座BC=0.60米,底座BC与支架AC所成的角∠ACB=75°,支架AF的长为2.50米,篮板顶端F点到篮框D的距离FD=1.35米,篮板底部支架HE与支架AF所成的角∠FHE=60°,求篮框D到地面的距离(精确到0.01米)(参考数据:cos75°≈0.2588,sin75°≈0.9659,tan75°≈3.732,![]() ≈1.732,
≈1.732,![]() ≈1.414)
≈1.414)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某一出租车一天下午以鼓楼为出发点在东西方向运营,向东走为正,向西走为负,行车里程(单位:km)依先后次序记录如下:![]() .
.
(1)将最后一名乘客送到目的地,出租车离鼓楼出发点多远?在鼓楼的什么方向?
(2)若每千米的价格为2.4元,司机一个下午的营业额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动手操作:
(1)如图1,将一块直角三角板DEF放置在直角三角板ABC上,使三角板DEF的两条直角边DE、DF分别经过点B、C,且BC∥EF,已知∠A=30°,则∠ABD+∠ACD= 度;
(2)如图2,∠BDC与∠A、∠B、∠C之间存在着什么关系,并说明理由;
(3)灵活应用:请你直接利用以上结论,解决以下列问题:如图3,BE平分∠ABD,CE平分∠ACD,若∠BAC=40°,∠BDC=120°,求∠BEC的度数。



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com