
����Ŀ��ijУΪ���˽ⱾУ���꼶ѧ����������������������Ϊ�������ӣ���Ƚ��ӣ��жȽ��ӣ��ضȽ��ӣ�������Ծ��꼶�IJ���ѧ�������˳������飬�������������������������²�������ͳ��ͼ�����в��������ضȽ��������ĺ����жȽ���������2����

�������������Ϣ����������⣺
��1���ε����ѧ��������
��2����ȫ����ͳ��ͼ��������ͳ��ͼ�У�������������Ӧ���ε�Բ�ĽǶ�������144���ȣ�
��3������У���꼶ѧ����1050�ˣ�������Ƹ�У���꼶���ӣ�������Ƚ��ӣ��жȽ��ӣ��ضȽ��ӣ���ѧ����Լ�ж����ˣ�
���𰸡�
�������������������1��������Ƚ��ӵ�������14�ˣ�ռ��������28%�����������������
��2�����жȽ��ӵ�������x�ˣ��������ضȽ��������ĺ�2x���з������x��ֵ��������ò����ӵ�������Ȼ������360�����Զ�Ӧ�İٷֱȼ������Բ�ĽǵĶ�����
��3���������������Զ�Ӧ�İٷֱȼ�����⣮
�����������1�����ε����ѧ�����ǣ�14��28%=50���ˣ���
��2�����жȽ��ӵ�������x�ˣ��������ضȽ��������ĺ�2x����x+2x+14=50��
��ã�x=12��
���жȽ��ӵ�������12�������ӵ������ǣ�24��4=20���ˣ���
��������������Ӧ���ε�Բ�ĽǶ����ǣ�360���![]() =144����
=144����
��3��1050��![]() =630���ˣ���
=630���ˣ���
�𣺸�У���꼶���ӣ�������Ƚ��ӣ��жȽ��ӣ��ضȽ��ӣ���ѧ����Լ630�ˣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��ACΪ��O��ֱ����PA��AC��BC�ǡ�O��һ���ң�ֱ��PB��ֱ��AC�ڵ�D��![]() .��1����֤��ֱ��PB�ǡ�O�����ߣ�
.��1����֤��ֱ��PB�ǡ�O�����ߣ�
��2����cos��BCA�ĵ�ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��ѧ��ȤС��Ϊ�˽ⱾУѧ���Ե��ӽ�Ŀ��ϲ���������������˲���ѧ����ϲ����һ���Ŀ���������ѧ��ֻѡһ�ಢ��û�в�ѡ��ģ��������������Ƴ������µ�����ͳ��ͼ�������������������ͼ�����ṩ����Ϣ������������⣺

��1�����ε����ѧ������Ϊ__________�����ֽ�Ŀ������ͳ��ͼ����ռԲ�ĽǵĶ�����__________�ȣ�
��2���뽫����ͳ��ͼ����������
��3��������ѧ��2000��ѧ��������Ƹ�Уϲ��������Ŀ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() ����
����![]() ���߶�
���߶�![]() �ӳ���һ�㣬����
�ӳ���һ�㣬����![]() ��
��![]() ��
��![]()
��1�����߶�![]() ��������
��������![]() �˶���ʹ�õ�
�˶���ʹ�õ�![]() ���
���![]() �غϣ��ô���ʽ��ʾ�߶�
�غϣ��ô���ʽ��ʾ�߶�![]() ɨ����ƽ�沿�ֵ����.
ɨ����ƽ�沿�ֵ����.
��2����������![]() ���ŵ�
���ŵ�![]() ��ת��ʹ��
��ת��ʹ��![]() ��
��![]() �غϣ���
�غϣ���![]() ���ڵ�
���ڵ�![]() ���ô���ʽ��ʾ�߶�
���ô���ʽ��ʾ�߶�![]() ɨ����ƽ�沿�ֵ����.
ɨ����ƽ�沿�ֵ����.
��3����������![]() ˳ʱ����ת��ʹ��ת�����������һ���������ε�һ����ȫ�غϣ��ڣ�2��С���������⣩��������ͼ�л�������������3���������д����Ӧ����ת���ĺ���ת��
˳ʱ����ת��ʹ��ת�����������һ���������ε�һ����ȫ�غϣ��ڣ�2��С���������⣩��������ͼ�л�������������3���������д����Ӧ����ת���ĺ���ת��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ��������֣�����������Ϣ����������⣺�Ѽ������ô��������������м��ö��Ÿ������磺{3��4}��{��3��6��8��18}�����д������ڵ�������Ϊ���ϵ�Ԫ�أ����һ���������㣺ֻҪ������һ��Ԫ��a��ʹ�é�2a+4Ҳ��������ϵ�Ԫ�أ������ļ��ϳ�Ϊ�������ϣ����磻{3����2}����Ϊ��2��3+4����2����2ǡ����������ϵ�Ԫ��������{3����2}���������ϣ����磻����2��9��8��}����Ϊ��2������2��+4��8��8ǡ����������ϵ�Ԫ�أ�����{��2��9��8��}���������ϣ�
��1������{��4��12}�Ƿ����������ϣ�
��2������{![]() ����
����![]() ��
��![]() }�Ƿ����������ϣ�
}�Ƿ����������ϣ�
��3��������{8��n}��{m}�����������ϣ���m��n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ţ��ij��O��ʼ�ض�������ֱ�����У��涨�����е�·�̼�Ϊ�������������е�·�̼�Ϊ���������еĸ���·������Ϊ����λ�����ף���![]() .�ʣ�
.�ʣ�
��1����ţ����Ƿ�ص�������O��
��2����ţ�뿪������O��Զ�Ƕ������ף�
��3�������й����У����ÿ����1������һ��֥�飬����ţ�ɵõ�������֥�飿
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����̥��ֱ���Ƿ���ϱ������ж���̥�����ĺ�������Ҫ����֮һ��������̥��ij����̥�ı�ֱ����600mm����������Ա��������Ʒ�г�ȡ10����̥���м�飬������ֱ���ĺ�������Ϊ��������ĺ�������Ϊ��������¼���£���λ��mm����
��� | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
����� |
|
|
| 0 |
|
|
|
|
|
|
��
��2������10����̥��ƽ��ֱ������ȷ��![]() mm����
mm����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
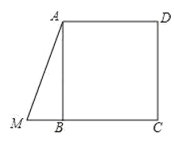
����Ŀ���ھ���ABCD�У�FΪAD���е㣬DE��![]() ��CF��BD�ֱ�BD��AD�ڵ�E��F������BF.
��CF��BD�ֱ�BD��AD�ڵ�E��F������BF.
��1����֤��EC��2EF��
��2�����ı���BCDF�����.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
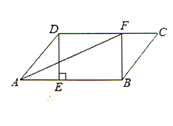
����Ŀ������ABCD�У�����D��DE��AB�ڵ�E����F��CD�ϣ�CF=AE������BF��AF��
��1����֤���ı���BFDE�Ǿ��Σ�
��2����AFƽ�֡�BAD����AE=3��DE=4�������BFDE�������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com