
【题目】如图所示,AC为⊙O的直径且PA⊥AC,BC是⊙O的一条弦,直线PB交直线AC于点D,![]() .(1)求证:直线PB是⊙O的切线;
.(1)求证:直线PB是⊙O的切线;
(2)求cos∠BCA的的值.

【答案】(1)证明见解析;(2)cos∠BCA =![]()
【解析】分析:(1)连接OB、OP,如图,结合相似三角形的性质可推出△BDC∽△PDO,进一步分析可得BC∥OP,由此通过角之间的等量转化便不难得到△BOP≌△AOP,至此结合全等三角形的性质,问题(1)便可得以解决;
(2)设PB=a,则BD=2a,根据切线长定理得到PA=PB=a,由此借助勾股定理以及线段间的比例关系即可用含a的代数式表示出OP以及OA的长.
详解:(1)证明:连接OB、OP .
∵ ![]() 且∠D=∠D,
且∠D=∠D,
∴ △BDC∽△PDO ,
∴ ∠DBC=∠DPO ,
∴ BC∥OP,
∴ ∠BCO=∠POA , ∠CBO=∠BOP.
∵ OB=OC ,
∴ ∠OCB=∠CBO ,
∴ ∠BOP=∠POA.
又∵ OB=OA, OP=OP ,
∴ △BOP≌△AOP ,
∴ ∠PBO=∠PAO.
又∵ PA⊥AC ,
∴ ∠PBO=90° ,
∴ 直线PB是⊙O的切线.
(2)由(1)知∠BCO=∠POA ,
设PB![]() ,则
,则![]() .
.
又∵ ![]() ,
,
∴ ![]() .
.
又∵ BC∥OP ,
∴ ![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴ cos∠BCA=cos∠POA=![]() .
.


科目:初中数学 来源: 题型:
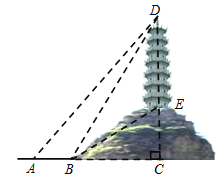
【题目】如图,某人为了测量小山顶上的塔ED的高,他在山下的点A处测得塔尖点D的仰角为45°,再沿AC方向前进60m到达山脚点B,测得塔尖点D的仰角为60°,塔底点E的仰角为30°,求塔ED的高度.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面上,Rt△ABC与直径为CE的半圆O如图1摆放,∠B=90°,AC=2CE=m,BC=n,半圆O交BC边于点D,将半圆O绕点C按逆时针方向旋转,点D随半圆O旋转且∠ECD始终等于∠ACB,旋转角记为α(0°≤α≤180°)
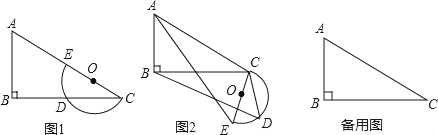
(1)当α=0°时,连接DE,则∠CDE= °,CD= ;
(2)试判断:旋转过程中![]() 的大小有无变化?请仅就图2的情形给出证明;
的大小有无变化?请仅就图2的情形给出证明;
(3)若m=10,n=8,当α=∠ACB时,求线段BD的长;
(4)若m=6,n=4![]() ,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
,当半圆O旋转至与△ABC的边相切时,直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量某建筑物CD的高度,先在地面上用测角仪自A处测得建筑物顶部的仰角是30°,然后在水平地面上向建筑物前进了100 m,此时自B处测得建筑物顶部的仰部角是45°.已知测角仪的高度是1.5 m,请你计算出该建筑物的高度.(取≈1.732,结果精确到1 m)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以Rt△ABC的直角边AC及斜边AB向外作等边△ACD及等边△ABE.已知∠BAC=30°,EF⊥AB,垂足为F,连接DF.
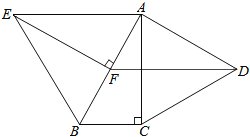
(1)试说明AC=EF;
(2)求证:四边形ADFE是平行四边形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红帮弟弟荡秋千(如图1),秋千离地面的高度h(m)与摆动时间t(s)之间的关系如图2所示.
(1)根据函数的定义,请判断变量h是否为关于t的函数?
(2)结合图象回答:
①当![]() 时,h的值大约是多少?并说明它的实际意义.
时,h的值大约是多少?并说明它的实际意义.
②秋千摆动第二个来回需多少时间?


图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
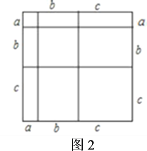
【题目】我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如图![]() 可以得到
可以得到![]()
![]() .请解答下列问题:
.请解答下列问题:
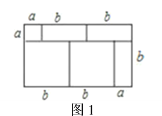
(1)写出图![]() 中所表示的数学等式;
中所表示的数学等式;
(2)利用(1)中所得到的结论,解决下面的问题:已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)小明同学打算用![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张边长为
张边长为![]() 的正方形,
的正方形,![]() 张相邻两边长为分别为
张相邻两边长为分别为![]() 、
、![]() 的长方形纸片拼出了一个面积为
的长方形纸片拼出了一个面积为 ![]() 长方形,那么他总共需要多少张纸片?
长方形,那么他总共需要多少张纸片?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解本校九年级学生的视力情况(视力情况分为:不近视,轻度近视,中度近视,重度近视),随机对九年级的部分学生进行了抽样调查,将调查结果进行整理后,绘制了如下不完整的统计图,其中不近视与重度近视人数的和是中度近视人数的2倍.

请你根据以上信息解答下列问题:
(1)求本次调查的学生人数;
(2)补全条形统计图,在扇形统计图中,“不近视”对应扇形的圆心角度数是 144 度;
(3)若该校九年级学生有1050人,请你估计该校九年级近视(包括轻度近视,中度近视,重度近视)的学生大约有多少人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com