
����Ŀ����ͼ���ڱ߳�Ϊ4��������ABCD�У�P��BC����һ���㣨����B��C���㣩������ABP��ֱ��AP���ۣ���B���ڵ�E������CD����һ��M��ʹ�ý���CMP��ֱ��MP���ۺ�C����ֱ��PE�ϵĵ�F����ֱ��PE��CD�ڵ�N������MA��NA�������½�������ȷ������д��������ȷ���۵���ţ�
�١�CMP�ס�BPA��
���ı���AMCB��������ֵΪ10��
�۵�PΪBC�е�ʱ��AEΪ�߶�NP���д��ߣ�
���߶�AM����СֵΪ2 ![]() ��
��
�ݵ���ABP�ա�ADNʱ��BP=4 ![]() ��4��
��4��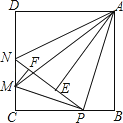
���𰸡��٢ڢ�
���������⣺�ߡ�APB=��APE����MPC=��MPN��
�ߡ�CPN+��NPB=180�㣬
��2��NPM+2��APE=180�㣬
���MPN+��APE=90�㣬
���APM=90�㣬
�ߡ�CPM+��APB=90�㣬��APB+��PAB=90�㣬
���CPM=��PAB��
���ı���ABCD�������Σ�
��AB=CB=DC=AD=4����C=��B=90�㣬
���CMP�ס�BPA���ʢ���ȷ��
��PB=x����CP=4��x��
�ߡ�CMP�ס�BPA��
�� ![]() =
= ![]() ����CM=
����CM= ![]() x��4��x������S�ı���AMCB=
x��4��x������S�ı���AMCB= ![]() [4+
[4+ ![]() x��4��x��]��4=��
x��4��x��]��4=�� ![]() x2+2x+8=��
x2+2x+8=�� ![]() ��x��2��2+10��
��x��2��2+10��
��x=2ʱ���ı���AMCB������ֵΪ10���ʢ���ȷ��
��PB=PC=PE=2ʱ����ND=NE=y��
��RT��PCN����y+2��2=��4��y��2+22���y= ![]() ��
��
��NE��EP���ʢ۴���
��MG��AB��G��
��AM= ![]() =
= ![]() ��
��
��AG��СʱAM��С��
��AG=AB��BG=AB��CM=4�� ![]() x��4��x��=
x��4��x��= ![]() ��x��1��2+3��
��x��1��2+3��
��x=1ʱ��AG��Сֵ=3��
��AM����Сֵ= ![]() =5���ʢܴ���
=5���ʢܴ���
�ߡ�ABP�ա�ADNʱ��
���PAB=��DAN=22.5�㣬��AB��ȡһ��Kʹ��AK=PK����PB=z��
���KPA=��KAP=22.5��
�ߡ�PKB=��KPA+��KAP=45�㣬
���BPK=��BKP=45�㣬
��PB=BK=z��AK=PK= ![]() z����z+
z����z+ ![]() z=4����z=4
z=4����z=4 ![]() ��4����PB=4
��4����PB=4 ![]() ��4�ʢ���ȷ��
��4�ʢ���ȷ��
�ʴ�Ϊ�٢ڢݣ�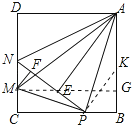
����ȷ��ֻҪ֤����APM=90�㼴�ɽ�����⣮
����ȷ����PB=x���������κ��������ö��κ������ʽ�����⼴�ɣ�
�۴�����ND=NE=y����RT��PCN�У����ù��ɶ������y���ɽ�����⣮
�ܴ�����MG��AB��G����ΪAM= ![]() =
= ![]() ������AG��СʱAM��С���������κ��������AG����СֵΪ3��AM����СֵΪ5��
������AG��СʱAM��С���������κ��������AG����СֵΪ3��AM����СֵΪ5��
����ȷ����AB��ȡһ��Kʹ��AK=PK����PB=z���г����̼��ɽ�����⣮���⿼���������ۺ��⡢�����ε����ʡ����������ε��ж������ʡ�ȫ�������ε����ʡ����ɶ�����֪ʶ������Ĺؼ���ѧ�ṹ�����κ��������ֵ���⣬ѧ�����ӳ��ø����ߣ������п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������μ����е���̨��֯�ġ�ĵ���������������Ŀ��������������ѡ���˳��ͨ�أ���һ����ѡ����3��ѡ��ڶ�����ѡ����4��ѡ��������������ᣬ���������������������������ã�ʹ�á�������һ�ο�����������ȥ������һ���һ������ѡ���
��1������������Ρ����������ڵ�һ������ʹ�ã���ô����ͨ�صĸ����� ��
��2������������Ρ����������ڵڶ�������ʹ�ã���ô����ͨ�صĸ����� ��
��3���������ÿ�������һ�Ρ���������������״ͼ�����б���������˳��ͨ�صĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���B=90�㣬��A=30�㣬�Ե�AΪԲ�ģ�BC��Ϊ�뾶������AB�ڵ�D���ֱ��Ե�A��DΪԲ�ģ�AB��Ϊ�뾶�������������ڵ�E������AE��DE�����EAD������ֵ�ǣ� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һЩ��ͬ��С�������ɵļ����������ͼ����ͼ��ͼ��ʾ������������Ϳ��һ�ָü����������ͼ����ʹ������ͼ����Գ�ͼ�Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪k=![]() ����
����![]() +n2+9=6n��������Ա���x��һ�κ���y=kx+m+n��ͼ��һ�������ڣ����������ޣ�
+n2+9=6n��������Ա���x��һ�κ���y=kx+m+n��ͼ��һ�������ڣ����������ޣ�
A.һ����
B.������
C.������
D.һ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������Щ���ӵ�ͼ��������һ��ͼ���Ļ����ϣ��ڡ����λ��塱�������϶�һ����γɵģ�������ÿһ��ͼ����������һ��������ͼ����ͨ��������ת��������ת�ĽǶ��ǣ� ��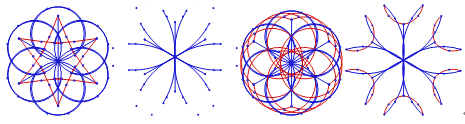
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ABC��ƽ��ֱ������ϵ�е�λ����ͼ��ʾ����֪��A����6��0������B��ԭ�㣬CA=CB=5���ѵ���������ABC��x��������������˳ʱ�뷭ת����һ�η�ת��λ�â٣��ڶ��η�ת��λ�âڡ����˹��ɣ���15�η�ת���C�ĺ������� �� 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx��a��0������ԭ��O�͵�A��2��0���� 
��1��д�������ߵĶԳ�����x��Ľ������ꣻ
��2���㣨x1 �� y1������x2 �� y2�����������ϣ���x1��x2��1���Ƚ�y1 �� y2�Ĵ�С��
��3����B����1��2���ڸ��������ϣ���C���B���������ߵĶԳ���Գƣ���ֱ��AC�ĺ�����ϵʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�DEƽ�֡�ADC��AB�ڵ�E��BFƽ�֡�ABC����CD�ڵ�F�� 
��1����֤��DE=BF��
��2������EF��д��ͼ�����е�ȫ�������Σ�����Ҫ��֤����
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com