
【题目】已知k=![]() ,且
,且![]() +n2+9=6n,则关于自变量x的一次函数y=kx+m+n的图象一定经过第( )象限.
+n2+9=6n,则关于自变量x的一次函数y=kx+m+n的图象一定经过第( )象限.
A.一、二
B.二、三
C.三、四
D.一、四
【答案】A
【解析】首先由![]() +n2+9=6n,根据二次根式和完全平方式确定m n的值,再由k=
+n2+9=6n,根据二次根式和完全平方式确定m n的值,再由k=![]() ,利用比例的性质确定K的值,根据函数的图象特点即可判断出选项.
,利用比例的性质确定K的值,根据函数的图象特点即可判断出选项.![]() +n2+9=6n,
+n2+9=6n,![]() =﹣(n﹣3)2 ,
=﹣(n﹣3)2 ,
∴m=5,n=3,
∵k=![]()
∴a+b﹣c=ck,a﹣b+c=bk,﹣a+b+c=ak,
相加得:a+b+c=(a+b+c)k,
当a+b+c=0时,k为任何数,
当a+b+c≠0时,k=1,
即:y=kx+8或y=x+8,
所以图象一定经过一二象限.
故选A.
【考点精析】通过灵活运用一次函数的性质和比例的性质,掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;基本性质;更比性质(交换比例的内项或外项);反比性质(交换比的前项、后项);等比性质即可以解答此题.


科目:初中数学 来源: 题型:
【题目】如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( ) 
A.不变
B.增大
C.减小
D.先变大再变小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
(1)求MP的值
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将△ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的有(写出所有正确结论的序号)
①△CMP∽△BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2 ![]() ;
;
⑤当△ABP≌△ADN时,BP=4 ![]() ﹣4.
﹣4.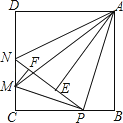
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,AB=CD,点E、F在BC上,且BE=CF. 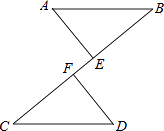
(1)求证:△ABE≌△DCF;
(2)试证明:以A、F、D、E为顶点的四边形是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com