
【题目】如图,抛物线y=ax2+bx(a≠0)过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)求点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,是否存在这样的点P,使得△ABP的面积为△ABC面积的2倍?若存在,求出点P的坐标,若不存在,请说明理由.

【答案】(1)y=﹣x2+4x;(2)3(3)P点坐标为(5,﹣5)
【解析】
(1)把A点和B点坐标分别代入y=ax2+bx中得到关于a、b的方程组,然后解方程组即可得到抛物线解析式;
(2)计算函数值为3所对应的自变量的值即可得到C点横坐标,然后根据三角形面积公式计算△ABC的面积;
(3)作PQ⊥BH于Q,如图,设P(m,-m2+4m),则利用S△ABH+S梯形APQH=S△PBQ+S△ABP可得到关于m的方程,然后解方程求出m即可得到P点坐标.
(1)把A(4,0),B(1,3)代入y=ax2+bx得
![]() ,解得
,解得![]() ,
,
所以抛物线解析式为y=﹣x2+4x;
(2)当y=3时,﹣x2+4x=3,解得x1=1,x2=3,
则C点坐标为(3,3),
所以△ABC的面积=![]() ×2×3=3;
×2×3=3;
(3)作PQ⊥BH于Q,如图,设P(m,﹣m2+4m).
∵S△ABH+S梯形APQH=S△PBQ+S△ABP,
∴![]() ×3×3+
×3×3+![]() (3+m﹣1)×(m2﹣4m)=
(3+m﹣1)×(m2﹣4m)=![]() ×(m﹣1)×(3+m2﹣4m)+2×3,
×(m﹣1)×(3+m2﹣4m)+2×3,
整理得m2﹣5m=0,解得m1=0(舍去),m2=5,
∴P点坐标为(5,﹣5).


 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,下列图形都是由面积为1的正方形按一定的规律组成,其中,第(1)个图形中面积为1的正方形有2个,第(2)个图形中面积为1的正方形有5个,第(3)个图形中面积为1的正方形有9个,……按此规律,则第50个图形中面积为1的正方形的个数为( )

A. 1322 B. 1323 C. 1324 D. 1325
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 某新建成学校举行“美化绿化校园”活动,计划购买A、B两种花木共300棵,其中A花木每棵20元,B花木每棵30元.
(1)若购进A,B两种花木刚好用去7300元,则购买了A,B两种花木各多少棵?
(2)如果购买B花木的数量不少于A花木的数量的1.5倍,且购买A、B两种花木的总费用不超过7820元,请问学校有哪几种购买方案?哪种方案最省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,证明:△ABD≌△ACE,DE=BD+CE;
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D, A, E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E是直线AB、CD外一点,直线AB和ED相交于点F.

(1)如果AB∥CD,那么∠D=∠B+∠E吗?
(2)如果∠D=∠B+∠E,那么AB与CD平行吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了编撰祖国的优秀传统文化,某校组织了一次“诗词大会”,小明和小丽同时参加,其中,有一道必答题是:从如图所示的九宫格中选取七个字组成一句唐诗,其答案为“山重水复疑无路”.
(1)小明回答该问题时,对第二个字是选“重”还是选“穷”难以抉择,若随机选择其中一个,则小明回答正确的概率是 ;
(2)小丽回答该问题时,对第二个字是选“重”还是选“穷”、第四个字是选“富”还是选“复”都难以抉择,若分别随机选择,请用列表或画树状图的方法求小丽回答正确的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
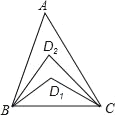
【题目】如图,在△ABC中,∠A=20°,∠ABC与∠ACB的角平分线交于D1,∠ABD1与∠ACD1的角平分线交于点D2,依此类推,∠ABD4与∠ACD4的角平分线交于点D5,则∠BD5C的度数是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com