
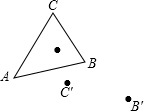
 如图所示,小明在黑板上画△ABC绕一点P旋转45°角的旋转图时,当他完成B,C两点分别旋转到点B′,C′时,不小心把旋转中心擦掉了,没有了旋转中心,小明不知道如何画下去,你能帮助他画完图形吗?
如图所示,小明在黑板上画△ABC绕一点P旋转45°角的旋转图时,当他完成B,C两点分别旋转到点B′,C′时,不小心把旋转中心擦掉了,没有了旋转中心,小明不知道如何画下去,你能帮助他画完图形吗? 分析 根据旋转的性质PC=PC′,PB=PB′,则点P为CC′和BB′的垂直平分线的交点,这样可确定P点位置,连结BP和B′P,根据旋转的性质得∠A′PA和∠B′PB都等于旋转角,所以作∠A′PA=∠B′PB,再截取A′P=AP即可得到A′点的位置,从而得到A′B′C′.
解答 解:连结CC′、BB′,作CC′和BB′的垂直平分线相交于点P,
连结BP和B′P,作∠A′PA=∠B′PB,再截取A′P=AP,则点A′为点A的对应点,
连结A′B′,A′C′,B′C′,则△A′B′C′为△ABC绕点P旋转45°角所得的三角形.
如图所示: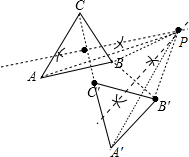
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:解答题
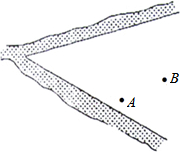 已知A村和B村坐落在两相交公路内(如图所示),为繁荣当地经济,A、B两付计划合建一座物流中心,要求所建物流中心必须满足下列条件:①到两条公路的距离相等;②到A、B两村的距离也相等.
已知A村和B村坐落在两相交公路内(如图所示),为繁荣当地经济,A、B两付计划合建一座物流中心,要求所建物流中心必须满足下列条件:①到两条公路的距离相等;②到A、B两村的距离也相等.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com