
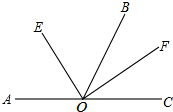
 如图,AC为一条直线,O是AC上一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC.
如图,AC为一条直线,O是AC上一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC.分析 (1)根据角平分线的定义求得∠BOE和∠BOF,然后根据∠EOF=∠BOE+∠BOF求解;
(2)根据角平分线的定义∠BOE=$\frac{1}{2}$∠AOB,∠BOF=$\frac{1}{2}$∠BOC,则∠EOF=∠BOE+∠BOF=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOB+∠BOC),据此即可求解.
解答 解:(1)∵OE平分∠AOB,
∴∠BOE=$\frac{1}{2}$∠AOB=$\frac{1}{2}$×120°=60°,
又∵∠BOC=180°-∠AOB=180°-120°=60°,OF平分∠BOC,
∴∠BOF=$\frac{1}{2}$∠BOC=$\frac{1}{2}$×60°=30°,
∴∠EOF=∠BOE+∠BOF=60°+30°=90°;
(2)∠EOF大小不变.
理由是:∵OE平分∠AOB,OF平分∠BOC,
∴∠BOE=$\frac{1}{2}$∠AOB,
∴∠BOF=$\frac{1}{2}$∠BOC,
∴∠EOF=∠BOE+∠BOF=$\frac{1}{2}$∠AOB+$\frac{1}{2}$∠BOC=$\frac{1}{2}$(∠AOB+∠BOC)=$\frac{1}{2}$×180°=90°.
点评 本题考查了角度的计算,理解角平分线的定义是解决本题的关键.


科目:初中数学 来源: 题型:填空题
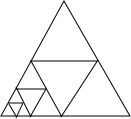 如图,在三角形中的一个最小单元(第一次是大三角形本身)内画三条线段将其分割成四等份,当进行到第15次的时候,图中共61个三角形;当进行到第n次的时候,图中共有多少个三角形?
如图,在三角形中的一个最小单元(第一次是大三角形本身)内画三条线段将其分割成四等份,当进行到第15次的时候,图中共61个三角形;当进行到第n次的时候,图中共有多少个三角形?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增减 | +5 | -2 | -4 | +12 | -10 | +16 | -9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
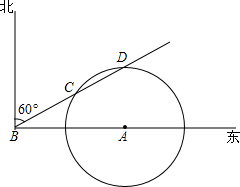 如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.
如图,在气象站台A的正西方向320km的B处有一台风中心,该台风中心以每小时20km的速度沿北偏东60°的BD方向移动,在距离台风中心200km内的地方都要受到其影响.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com