
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
分析 根据等式的两边同时加上(或减去)同一个数(或字母),等式仍成立;等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立.
解答 解:①由x=1,得x2=x两边都乘以x,故①正确;
②由$\frac{b}{a}$=$\frac{c}{a}$,得b=c两边都乘以a,故②正确;
③由a2=3a,得a=3,a=0时不成立,故③错误;
④由a=b,得$\frac{a}{{c}^{2}+1}$=$\frac{b}{{c}^{2}+1}$两边都除以(c2+1),故④正确;
⑤由m=n,得1-m=n-1左边乘以-1,加1,右边减1,故⑤错误;
⑥由x=y,得3-2x=3-2y两边都乘以-2,两边都加3,故⑥正确;
故选:B.
点评 本题主要考查了等式的基本性质,等式的两边同时加上(或减去)同一个数(或字母),等式仍成立;等式的两边同时乘以(或除以)同一个不为0数(或字母),等式仍成立.


 ABC考王全优卷系列答案
ABC考王全优卷系列答案科目:初中数学 来源: 题型:解答题
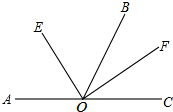 如图,AC为一条直线,O是AC上一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC.
如图,AC为一条直线,O是AC上一点,∠AOB=120°,OE、OF分别平分∠AOB和∠BOC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
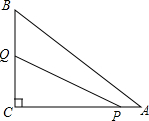 如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,当点P停止运动时,点Q也随之停止,点P,Q同时出发,设点P的运动时间为t(秒).
如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,点P从点A出发,沿AC以每秒1个单位的速度向终点C运动,点Q从点C出发,沿C-B-A以每秒2个单位的速度向终点A运动,当点P停止运动时,点Q也随之停止,点P,Q同时出发,设点P的运动时间为t(秒).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )
如图所示,在平行四边形ABCD中,AC与BD相交于点O,E为OD的中点,连接AE并延长交DC于点F,则DF:FC=( )| A. | 1:3 | B. | 1:4 | C. | 2:3 | D. | 1:2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com