
分析 (1)推出2016年11月14日是星期一,即可解决问题;
(2)火曜日为星期二,而10月里4、11、18、25号为星期二,由此即可解决问题;
(3)用余数定理即可解决问题;
解答 解:(1)∵2016年11月14日是星期一,
∴2016年11月14日是“七曜日”中的月曜日.
故答案为:月.
(2)∵火曜日为星期二,而10月里4、11、18、25号为星期二,
∴2016年10月的几个“火曜日”分别是4、11、18、25号.
(3)用3除余2,用7除也余2,所以用3与7的最小公倍数21除也余2,而用21除余2的数我们首先就会想到23;23恰好被5除余3,所以23就是本题的一个答案.
故答案为23.
点评 本题考查日历问题、余数定理等知识,解题的关键是理解题意,灵活运用所学知识解决问题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:选择题
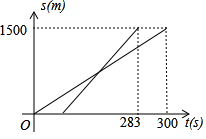 甲、乙两名同学在一次晨跑练习中都以各自的速度匀速跑,路程s(m)和时间t(s)之间的函数图象如图所示(粗线为甲的路程与时间的函数图象,细线为乙的路程与时间的函数图象),小张根据图象得到了如下四个信息,期中错误的是( )
甲、乙两名同学在一次晨跑练习中都以各自的速度匀速跑,路程s(m)和时间t(s)之间的函数图象如图所示(粗线为甲的路程与时间的函数图象,细线为乙的路程与时间的函数图象),小张根据图象得到了如下四个信息,期中错误的是( )| A. | 这是一次1500m的赛跑 | B. | 甲、乙两人中先到达终点的是乙 | ||
| C. | 甲、乙同时起跑 | D. | 甲在这次赛跑中的速度为5m/s |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (x-4)2=17 | B. | (x-4)2=15 | C. | (x+4)2=15 | D. | (x+4)2=17 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com