练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．下列各式计算正确的是（　　）
    A．a+2a2=3a3B．（a+b）2=a2+ab+b2C．2（a-b）=2a-2bD．（2ab）2÷（ab）=2ab（ab≠0）

    分析 根据合并同类项对A进行判断；根据完全平方公式对B进行判断；利用去括号法则对C进行判断；根据积的乘方和同底数幂的除法对D进行判断．

    解答 解：A、a与2a2不是同类项，不能合并，所以A选项错误；
    B、（a+b）2=a2+2ab+b2，所以B选项错误；
    C、2（a-b）=2a-2b，所以C选项正确；
    D、（2ab）2÷（ab）=4a2b2÷ab=4ab，所以D选项错误．
    故选C．

    点评 本题考查了整式的除法：单项式除以单项式，把系数，同底数幂分别相除后，作为商的因式；对于只在被除式里含有的字母，则连同他的指数一起作为商的一个因式．也考查了合并同类项和完全平方公式．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．小明用《几何画板》画图，他先画了两条平行线AB、CD，然后在平行线间画了一点E，连接BE，DE后（如图①），它用鼠标左键点住点E，拖动后，分别得到如图②、③、④等图形，这时他突然一想，∠B、∠D与∠BED之间的度数有没有某种联系呢？接着小明同学通过利用《几何画板》的“度量角度”和“计算”的功能，找到了这三个角之间的关系．

    （1）请你分别写出图①至图④各图中的∠B、∠D与∠BED之间关系；
    （2）证明从图③中得到的结论．

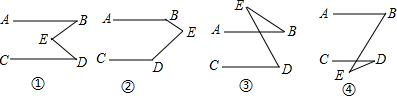
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

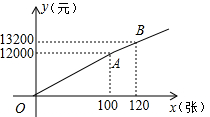    1．为了发展本地足球运动，在体育局的策划下，市体育馆将举行明星足球邀请赛，为此体育局推出两种购票方案（设购票张数为x，购票总价为y）：方案一：提供8 000元赞助后，每张票的票价为50元，方案二：票价按下图中的折线OAB所表示的函数关系确定．
    （1）若购买120张票时，按方案一和方案二分别应付的购票款是多少？
    （2）至少买多少张票时选择方案一比较合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．（1）填空：①（-xy2）2=x2y4，②（-x2）3÷（x2）2=-x2，③$（-3{x^2}y）（\frac{2}{3}x{y^2}）$=-2x3y3，④x（2x-1）=2x2-x．
    （2）计算：①（x+5y）（2x-y），②（-a）9÷（-a）6•a2+（2a4）2÷a3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列图形中既是轴对称图形又是中心对称图形的是（　　）
    A．等边三角形B．平行四边形C．菱形D．五角星

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．如图，EF∥BC，AC平分∠BAF，∠B=50°，则∠C的度数是（　　）
    A．50°B．55°C．60°D．65°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

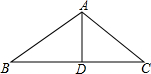    2．如图，厂房屋顶人字架的跨度BC=10m．D为BC的中点，上弦AB=AC，∠B=36°，求中柱AD和上弦AB的长（结果保留小数点后一位）．
    参考数据：sin36°≈0.59，cos36°≈0.81，tan36°≈0.73．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算：6.159×108（精确到万位）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知，P为函数y=$\frac{k}{|x|}$图象上的任意点．
    （1）如图1，若P点在第一象限．请分析函数y=$\frac{k}{|x|}$图象的对称性，并利用直尺和圆规在图1中作出P在图象上的对称点F（不写作法，保留作图痕迹）．
    （2）又若P1（a2+2，y1）、P2（a2，y2）、P3（-a2-1，y3）是函数y=$\frac{k}{|x|}$（k＞0）图象上的三点，请比较y1、y2、y3的大小，并说明理由．
    （3）使k=8，过点P分别作PC⊥x轴于C点，PK⊥y轴于K点，且PC交直线l：y=4x于点D，又使⊙P与y轴相切于点K，设⊙P的面积为S．试探究：
    ①如图2，连接KD、KC，若P在第一象限，试求出使△KPD与△KPC相似时S所有可能的取值？
    ②如图3，又若P不一定在第一象限．请写出⊙P 与直线l相切时，S的可能值．（不用写过程，直接写出结论）

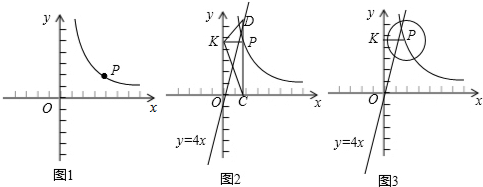
    查看答案和解析>>

    同步练习册答案