
【题目】抛物线![]() 与
与![]() 轴正半轴交于点
轴正半轴交于点![]() ,与
,与![]() 轴分别交于点
轴分别交于点![]() 和点
和点![]() 且
且![]() .
.
(1)求抛物线的解析式;
(2)点![]() 是
是![]() 轴上一点,当
轴上一点,当![]() 和
和![]() 相似时,求点
相似时,求点![]() 的坐标.
的坐标.
【答案】(1)y=![]() x2-
x2-![]() x+2(2)(0,
x+2(2)(0,![]() )或(0,-
)或(0,-![]() )
)
【解析】
(1)由题意得抛物线的对称轴为x=![]() ,再求出A点坐标,由
,再求出A点坐标,由![]() ,进而求出OC的长,即可求解;
,进而求出OC的长,即可求解;
(2)由△BOC∽△COA,得∠OCB=∠OAC,当![]() 和
和![]() 相似时,分两种情况:①
相似时,分两种情况:①![]() ,②
,②![]() ,分别求出符合题意的OP的长,即可得到P点坐标
,分别求出符合题意的OP的长,即可得到P点坐标
解:(1)由题意得抛物线的对称轴为x=![]() ,
,
∵点![]() 和点
和点![]() 关于对称轴对称,∴A(4,0)
关于对称轴对称,∴A(4,0)
∵![]() =4×1=4,
=4×1=4,
∴OC=2,
∴C(0,2)
∴![]()
解得:m=![]() ,n=2
,n=2
∴解析式为y=![]() x2-
x2-![]() x+2
x+2
(2)由题意,可得AB=3,BC=![]() ,AC=2
,AC=2![]() ,
,
∵![]() ,
,
∴![]() ,又∠BOC=∠COA
,又∠BOC=∠COA
∴△BOC∽△COA,
∴∠OCB=∠OAC,
∴当![]() 和
和![]() 相似时,分两种情况:
相似时,分两种情况:
①![]() 时,得
时,得![]() ,解得CP=
,解得CP=![]()
∴OP=OC-CP=2-![]() =
=![]()
∴P(0,![]() );
);
②![]() ,得
,得![]() ,解得CP=
,解得CP=![]()
∴OP=CP-OC=![]() -2=
-2=![]()
∴P(0,-![]() );
);
综上可得P的坐标为(0,![]() )或(0,-
)或(0,-![]() ).
).


科目:初中数学 来源: 题型:
【题目】在全民读书月活动中,某校随机调查了部分同学,本学期计划购买课外书的费用情况,并将结果绘制成如图所示的统计图.根据相关信息,解答下列问题.
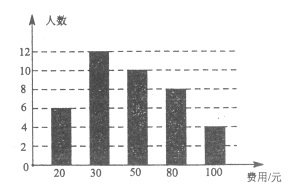
(Ⅰ)这次调查获取的样本容量是____________.(直接写出结果);
(Ⅱ)求这次调查获取的样本数据的众数,中位数,平均数;
(Ⅲ)若该校共有1000名学生,根据样本数据,估计该校本学期计划购买课外书的总花费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过点
经过点![]() ,
,
(Ⅰ)求抛物线的解析式;
(Ⅱ)过点![]() 作
作![]() 于点
于点![]() ,过抛物线上一动点
,过抛物线上一动点![]() (不与点
(不与点![]() 重合),作直线
重合),作直线![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() ,若以点
,若以点![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的横坐标.
的横坐标.
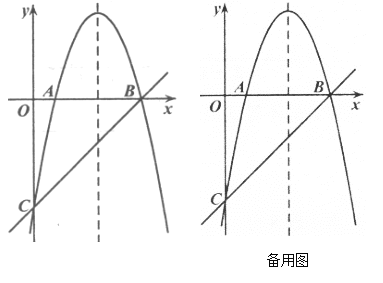
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,利用两面靠墙(墙足够长),用总长度37米的篱笆(图中实线部分)围成一个矩形鸡舍ABCD,且中间共留三个1米的小门,设篱笆BC长为x米.
(1)AB=______.(用含x的代数式表示)
(2)若矩形鸡舍ABCD 面积为150平方米,求篱笆BC的长.
(3)矩形鸡舍ABCD面积是否有可能达到210平方米?若有可能,求出相应x的值;若不可能,则说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣![]() x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
x2﹣x+4与x轴交于A,B两点(A在B的左侧),与y轴交于点C.
(1)求点A,点B的坐标;
(2)P为第二象限抛物线上的一个动点,求△ACP面积的最大值.
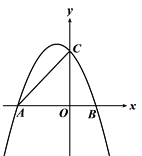
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年本市蜜桔大丰收,某水果商销售一种蜜桔,成本价为10元/千克,已知销售价不低于成本价,且物价部门规定这种产品的销售价不高于18元/千克,市场调查发现,该产品每天的销售量![]() (千克)与销售价
(千克)与销售价![]() (元/千克)之间的函数关系如图所示:
(元/千克)之间的函数关系如图所示:
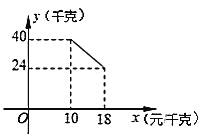
(1)求![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;
(2)该经销商想要每天获得150元的销售利润,销售价应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
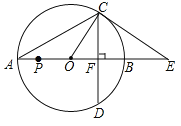
【题目】如图,以AB为直径的⊙O与CE相切于点C,CE交AB的延长线于点E,直径AB=18,∠A=30°,弦CD⊥AB,垂足为点F,连接AC,OC,则下列结论正确的是______.(写出所有正确结论的序号)
①![]() ;
;
②扇形OBC的面积为![]() π;
π;
③△OCF∽△OEC;
④若点P为线段OA上一动点,则APOP有最大值20.25.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)如图,自来水厂A和村庄B在小河l的两侧,现要在A,B间铺设一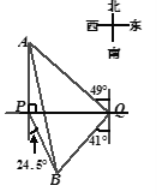 知输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏东49°方向,B位于南偏西41°方向.
知输水管道.为了搞好工程预算,需测算出A,B间的距离.一小船在点P处测得A在正北方向,B位于南偏东24.5°方向,前行1200m,到达点Q处,测得A位于北偏东49°方向,B位于南偏西41°方向.
(1)线段BQ与PQ是否相等?请说明理由;
(2)求A,B间的距离.(参考数据cos41°=0.75)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com