
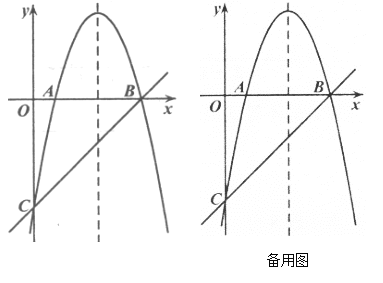
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过点
经过点![]() ,
,
(Ⅰ)求抛物线的解析式;
(Ⅱ)过点![]() 作
作![]() 于点
于点![]() ,过抛物线上一动点
,过抛物线上一动点![]() (不与点
(不与点![]() 重合),作直线
重合),作直线![]() 的平行线交直线
的平行线交直线![]() 于点
于点![]() ,若以点
,若以点![]() 为顶点的四边形是平行四边形,求点
为顶点的四边形是平行四边形,求点![]() 的横坐标.
的横坐标.
【答案】(Ⅰ)![]() ;(Ⅱ)点
;(Ⅱ)点![]() 的横坐标为4或
的横坐标为4或![]() 或
或![]() .
.
【解析】
(Ⅰ)利用一次函数解析式可得B、C两点坐标,再利用待定系数法求出抛物线的解析式即可;(Ⅱ)先解方程可求出A点坐标,根据B、C坐标可证明△OCB为等腰直角三角形,可求出AM的长,根据平行四边形的性质可得PQ=AM=2![]() ,PQ⊥BC,作
,PQ⊥BC,作![]() 轴交直线
轴交直线![]() 于
于![]() ,利用∠PDQ=45°可得PD=
,利用∠PDQ=45°可得PD=![]() PQ=4,设P(m,-m2+6m-5),则D(m,m-5),分别讨论P点在BC的上方时,PD=-m2+6m-5-(m-5)=4,P点在BC下方时,PD=(m-5)-( -m2+6m-5)=4,解方程求出m的值即可得P点横坐标.
PQ=4,设P(m,-m2+6m-5),则D(m,m-5),分别讨论P点在BC的上方时,PD=-m2+6m-5-(m-5)=4,P点在BC下方时,PD=(m-5)-( -m2+6m-5)=4,解方程求出m的值即可得P点横坐标.
(Ⅰ)当![]() 时,
时,![]() ,则
,则![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ,则
,则![]() .
.
把![]() 代入
代入![]() ,
,
得![]() .
.
解得![]()
∴抛物线解析式为![]() .
.
(Ⅱ)解方程![]() 得
得![]() ,则
,则![]() ,
,
∵![]() ,
,
∴![]() 为等腰直角三角形.
为等腰直角三角形.
∴![]() .
.
∵![]() ,
,
∴![]() 为等腰直角三角形.
为等腰直角三角形.
∴![]() .
.
∵以点![]() 为顶点的四边形是平行四边形,
为顶点的四边形是平行四边形,
∴![]() .
.
如图,作![]() 轴交直线
轴交直线![]() 于
于![]() ,则
,则![]() ,
,
∴![]() .
.
设![]() ,则
,则![]() ,
,
①当点![]() 在直线
在直线![]() 上方时,
上方时,
![]() ,
,
解得![]() (舍),
(舍),![]() .
.
②当点![]() 在直线
在直线![]() 下方时,
下方时,
![]() ,
,
解得![]() .
.
综上所述,点![]() 的横坐标为4或
的横坐标为4或![]() 或
或![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,举行抽奖活动,并规定:顾客每购买100元的商品,就可随机抽取一张奖劵,抽得奖券“紫气东来”、“花开富贵”、“吉星高照”,就可以分别获得100元、50元、20元的购物券,抽得“谢谢惠顾”不赠购物券;如果顾客不愿意抽奖,可以直接获得购物券10元.小明购买了100元的商品,他看到商场公布的前10000张奖券的抽奖结果如下:

(1)求“紫气东来”奖券出现的频率;
(2)请你帮助小明判断,抽奖和直接获得购物券,哪种方式更合算?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若反比例函数y=![]() 与一次函数y=2x-4的图象都经过点A(a,2).
与一次函数y=2x-4的图象都经过点A(a,2).
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)当反比例函数y=![]() 的值大于一次函数y=2x-4的值时,求自变量x的取值范围.
的值大于一次函数y=2x-4的值时,求自变量x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】铁岭“荷花节”举办了为期15天的“荷花美食”厨艺秀.小张购进一批食材制作特色美食,每盒售价为50元,由于食材需要冷藏保存,导致成本逐日增加,第x天(1≤x≤15且x为整数)时每盒成本为p元,已知p与x之间满足一次函数关系;第3天时,每盒成本为21元;第7天时,每盒成本为25元,每天的销售量为y盒,y与x之间的关系如下表所示:
第x天 | 1≤x≤6 | 6<x≤15 |
每天的销售量y/盒 | 10 | x+6 |
(1)求p与x的函数关系式;
(2)若每天的销售利润为w元,求w与x的函数关系式,并求出第几天时当天的销售利润最大,最大销售利润是多少元?
(3)在“荷花美食”厨艺秀期间,共有多少天小张每天的销售利润不低于325元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民的环保意识,社区工作人员在某小区随机抽取了若干名居民开展有奖问卷调查活动,并用得到的数据绘制了如下条形统计图(得分为整数,满分为10分,最低分为6分).请根据图中信息,解答下列问题:
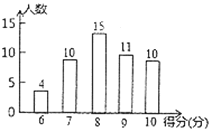
(Ⅰ)本次调查一共抽取了______名居民;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)如果对该小区的![]() 名居民全面开展这项有奖问答活动,得
名居民全面开展这项有奖问答活动,得![]() 分者设为一等奖,请你根据调查结果,帮社区工作人员估计需准备多少份一等奖奖品.
分者设为一等奖,请你根据调查结果,帮社区工作人员估计需准备多少份一等奖奖品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
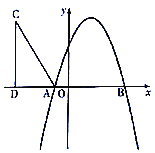
(1)求抛物线的解析式;
(2)在第二象限内取一点![]() ,作
,作![]() 垂直于
垂直于![]() 轴于点
轴于点![]() ,连接
,连接![]() ,且
,且![]() ,
,![]() ,将
,将![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位,当点
个单位,当点![]() 落在抛物线上时,求
落在抛物线上时,求![]() 的值;
的值;
(3)在(2)的条件下,当点![]() 第一次落在抛物线上时记为点
第一次落在抛物线上时记为点![]() ,点
,点![]() 是抛物线对称轴上一点.试探究:在抛物线上是否存在点
是抛物线对称轴上一点.试探究:在抛物线上是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,若存在,求出点
为顶点的四边形是平行四边形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某品牌太阳能热火器的实物图和横断面示意图,已知真空集热管![]() 与支架
与支架![]() 所在直线相交于水箱横断面
所在直线相交于水箱横断面![]() 的圆心
的圆心![]() ,支架
,支架![]() 与水平面
与水平面![]() 垂直,
垂直,![]() 厘米,
厘米,![]() ,另一根辅助支架
,另一根辅助支架![]() 厘米,
厘米,![]() .
.
(1)求垂直支架![]() 的长度;(结果保留根号)
的长度;(结果保留根号)
(2)求水箱半径![]() 的长度.(结果保留三个有效数字,参考数据:
的长度.(结果保留三个有效数字,参考数据:![]() )
)
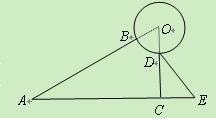
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com