
【题目】抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() (点
(点![]() 在点
在点![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() ,且
,且![]() ,
,![]() ,那么
,那么![]() 的值是_________.
的值是_________.
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() ,
,![]() 是常数,且
是常数,且![]() ),经过点
),经过点![]() ,
,![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(Ⅰ)求抛物线的解析式;
(Ⅱ)若点![]() 是射线
是射线![]() 上一点,过点
上一点,过点![]() 作
作![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() ,交抛物线于点
,交抛物线于点![]() ,设
,设![]() 点横坐标为
点横坐标为![]() ,线段
,线段![]() 的长为
的长为![]() ,求出
,求出![]() 与
与![]() 之间的函数关系式,并写出相应的自变量
之间的函数关系式,并写出相应的自变量![]() 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,当点![]() 在线段
在线段![]() 上时,设
上时,设![]() ,已知
,已知![]() ,
,![]() 是以
是以![]() 为未知数的一元二次方程
为未知数的一元二次方程![]() (
(![]() 为常数)的两个实数根,点
为常数)的两个实数根,点![]() 在抛物线上,连接
在抛物线上,连接![]() ,
,![]() ,
,![]() ,且
,且![]() 平分
平分![]() ,求出
,求出![]() 值及点
值及点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解居民的环保意识,社区工作人员在某小区随机抽取了若干名居民开展有奖问卷调查活动,并用得到的数据绘制了如下条形统计图(得分为整数,满分为10分,最低分为6分).请根据图中信息,解答下列问题:
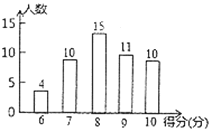
(Ⅰ)本次调查一共抽取了______名居民;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)如果对该小区的![]() 名居民全面开展这项有奖问答活动,得
名居民全面开展这项有奖问答活动,得![]() 分者设为一等奖,请你根据调查结果,帮社区工作人员估计需准备多少份一等奖奖品.
分者设为一等奖,请你根据调查结果,帮社区工作人员估计需准备多少份一等奖奖品.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点.
两点.
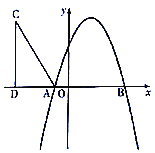
(1)求抛物线的解析式;
(2)在第二象限内取一点![]() ,作
,作![]() 垂直于
垂直于![]() 轴于点
轴于点![]() ,连接
,连接![]() ,且
,且![]() ,
,![]() ,将
,将![]() 沿
沿![]() 轴向右平移
轴向右平移![]() 个单位,当点
个单位,当点![]() 落在抛物线上时,求
落在抛物线上时,求![]() 的值;
的值;
(3)在(2)的条件下,当点![]() 第一次落在抛物线上时记为点
第一次落在抛物线上时记为点![]() ,点
,点![]() 是抛物线对称轴上一点.试探究:在抛物线上是否存在点
是抛物线对称轴上一点.试探究:在抛物线上是否存在点![]() ,使以点
,使以点![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,若存在,求出点
为顶点的四边形是平行四边形,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店销售一种进价为每本10元的笔记本,为获得高利润,以不低于进价进行销售,结果发现,每月销售量y与销售单价x之间的关系可以近似地看作一次函数:y=﹣5x+150,物价部门规定这种笔记本每本的销售单价不得高于18元.
(1)当每月销售量为70本时,获得的利润为多少元;
(2)该文具店这种笔记本每月获得利润为W元,求每月获得的利润W元与销售单价x之间的函数关系式,并写出自变量的取值范围;
(3)当销售单价定为多少元时,每月可获得最大利润,最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司5月份销售某种型号汽车,当月该型号汽车的进价为20万元/辆,若当月销售量超过5辆时,每多售出1辆,所有售出的汽车进价均降低0.1万元/辆.根据市场调查,月销售量不会突破40辆.
(1)设当月该型号汽车的销售量为![]() 辆(
辆(![]() ,且
,且![]() 为正整数),实际进价为
为正整数),实际进价为![]() 万元/辆,求
万元/辆,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)已知该型号汽车的销售价为22万元/辆,公司计划当月销售利润45万元,那么该月需售出多少辆汽车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△BCE中,点A是边BE上一点,以AB为直径的⊙O与CE相切于点D,AD∥OC,点F为OC与⊙O的交点,连接AF.
(1)求证:CB是⊙O的切线;
(2)若∠ECB=60°,AB=6,求图中阴影部分的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com