
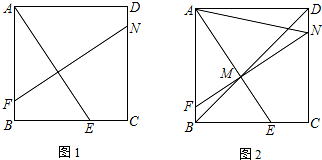
分析 (1)如图1,作平行线构造全等三角形,由全等三角形的对应边相等证得结论;
(2)如图2,作作MG⊥MD交DA的延长线于点G,证全等即可;
(3)如图3,求出线段BE、DN的长度后,再求三角形的面积.
解答 (1)证明:过点N作MN∥AD,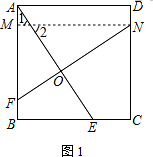
∵四边形ABCD为正方形,
∴∠DAM=∠D=90°,AD=AB=BC=CD,
∴∠AMN═90°,
∴四边形AMND是矩形,
∴MN=AD=AB,
∵NF⊥AE,
∴∠MNF+∠2=90°,
∵∠BAE+∠1=90°,∠1=∠2,
∴∠MNF=∠BAE,
在△MNF与△BAE中,
$\left\{\begin{array}{l}{∠MNF=∠BAE}\\{MN=BA}\\{∠NMF=∠ABE=90°}\end{array}\right.$,
∴△MNF≌△BAE(SAS),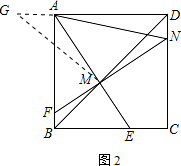
∴NF=AE;
(2)解:45°.
如图2,作MG⊥MD交DA的延长线于点G,
∵∠GDB=45°,MG⊥MD,
∴∠MGA=∠MDG=45°,MG=MD,
∵∠AMN=90°,
∴∠AMG=∠DMG-∠AMD=90°-∠AMD,∠NMD=∠AMN-∠AMD=90°-∠AMD,
∴∠AMG=∠NMD,
在△AGM与△DNM中,
$\left\{\begin{array}{l}{MGA=∠MDN=45°}\\{GM=DM}\\{∠GMA=∠DMB}\end{array}\right.$,
∴△AGM≌△DNM(SAS),
∴AM=NM,
∵∠AMN=90°,
∴△AMN为等腰直角三角形,
∴∠MAN=45°,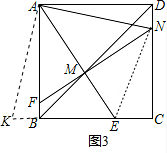
即∠EAN=45°;
(3)解:∵∠BAE=30°,AB=6,
∴BE=AB•tan30°=6×$\frac{\sqrt{3}}{3}$=2$\sqrt{3}$.
如图3,将△ADN绕点A顺时针旋转75°,得到△ABK.则S△ABK=S△ADN,AN=AK,DN=BK.
∵在△ADE与△ANE中,$\left\{\begin{array}{l}{AN=AK}\\{∠NAE=∠KAE=45°}\\{AE=AE}\end{array}\right.$,
∴△ADE≌△ANE(SAS),
∴NE=KE.
又∵在直角△ECN中,由勾股定理得到:NE2=CN2+CE2,
∴(BE+DN)2=CN2+CE2,即(2$\sqrt{3}$+DN)2=(6-DN)2+(6-2$\sqrt{3}$)2,
解得DN=12-6$\sqrt{3}$.
∴S△AEN=S□ABCD-S△ABE-S△ECN-S△ADN,
=6×6-$\frac{1}{2}$×6×2$\sqrt{3}$-$\frac{1}{2}$×(6-2$\sqrt{3}$)×(6-DN)-$\frac{1}{2}$×6×DN,
=18-$\sqrt{3}$DN,
=18-$\sqrt{3}$(12-6$\sqrt{3}$),
=36-12$\sqrt{3}$.
故答案是:36-12$\sqrt{3}$.
点评 本题考查了四边形综合题,此题涉及到了正方形的性质,全等三角形的判定与性质,三角形的面积公式以及等腰直角三角形的判定与性质,解题的难点是作出辅助线,构建全等三角形,利用全等三角形的判定与性质求得相关角的度数、相关线段的长度.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:初中数学 来源: 题型:选择题
| 成绩(分) | 80 | 82 | 84 | 86 | 87 | 90 |
| 人数 | 8 | 12 | 9 | 3 | 5 | 8 |
| A. | 82分,82分 | B. | 82分,83分 | C. | 80分,82分 | D. | 82分,84分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
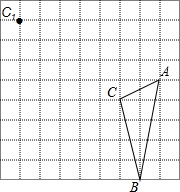 在边长为1的正方形网格中有△ABC,将这个三角形进行平移,使C点的对称点C1,
在边长为1的正方形网格中有△ABC,将这个三角形进行平移,使C点的对称点C1,查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2-4b≥0 | B. | a2-4b≠0 | ||
| C. | a2-4b<0 | D. | 与a,b取值有关,不能确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5 | B. | 4 | C. | 3 | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 与标准质量的差值(单位:g) | -5 | -2 | 0 | 1 | 3 | 6 |
| 袋数 | 1 | 4 | 3 | 4 | 5 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com