Question

【题目】从三角形（不是等腰三角形）一个顶点引出一条射线与对边相交，顶点与交点之间的线段把这个三角形分割成两个小三角形，如果分得的两个小三角形中有一个为等腰三角形，另一个与原三角形相似，我们把这条线段叫做这个三角形的完美分割线。

（1）如图1，在△ABC中，CD为角平分线，∠A=40°，∠B=60°，求证：CD为△ABC的完美分割线；

（2）在△ABC中，∠A=48°，CD是△ABC的完美分割线，且△ACD为等腰三角形，求∠ACB的度数；

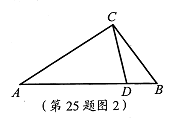
（3）如图2，△ABC中，AC=2，BC=，CD是△ABC的完美分割线，且△ACD是以CD为底边的等腰三角形，求完美分割线CD的长。

Answer 1

【答案】(1)详见解析；（2）∠ACB=96°或114°；（3）CD=.

【解析】

试题分析：（1）由∠A=40°，∠B=60°可得∠ACB=80°，即△ABC不是等腰三角形，再判定△ACD是等腰三角形，△BCD∽△BAC,即可得CD为△ABC的完美分割线；（2）分AD=CD，AD=AC，AC=CD三种情况，根据这三种情况分别求出∠ACB的度数，不合题意的舍去；(3)由△BCD∽△BAC可得，设BD=x，代入可得，由于x＞0，即可知x=-1.再由△BCD∽△BAC,所以，解得CD=.

试题解析：（1）∵∠A=40°，∠B=60°，

∴∠ACB=80°，

∴△ABC不是等腰三角形，

又因CD为角平分线，

∴∠ACD=∠BCD=∠ABC=40°，

∴∠ACD=∠A=40°，

∴△ACD是等腰三角形，

∵∠BCD=∠A=40°，∠B=∠B,

∴△BCD∽△BAC,

∴CD为△ABC的完美分割线；

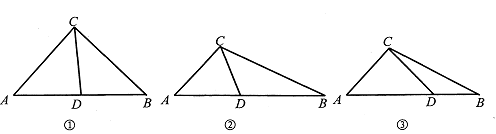
（2）当AD=CD时（如图①），∠ACD=∠A=48°，

∵△BDC∽△BCA,

∴∠BCD=∠A=48°，

∴∠ACB=∠ACD+∠BCD=96°；

当AD=AC时（如图②），∠ACD=∠ADC=，

∵△BDC∽△BCA,

∴∠BCD=∠A=48°，

∴∠ACB=∠ACD+∠BCD=114°；

当AC=CD时（如图③），∠ACD=∠A=48°，

∵△BDC∽△BCA,

∴∠BCD=∠A=48°，

∵∠ADC＞∠BCD，矛盾，舍去.

∴∠ACB=96°或114°；

（3）由已知AC=AD=2，

∵△BCD∽△BAC,

∴,

设BD=x

∴

解得x=-1±，

∵x＞0，

∴x=-1.

∵△BCD∽△BAC,

∴,

∴CD=.