
【题目】如图,已知抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() ,顶点为M.
,顶点为M.
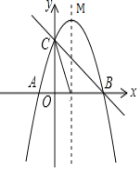
(1)求抛物线的解析式和点M的坐标;
(2)点E是抛物线段BC上的一个动点,设![]() 的面积为S,求出S的最大值,并求出此时点E的坐标;
的面积为S,求出S的最大值,并求出此时点E的坐标;
(3)在抛物线的对称轴上是否存在点P,使得以A、P、C为顶点的三角形是直角三角形?若存在,求出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ,M(1,4);(2)当
,M(1,4);(2)当![]() 时,S最大=
时,S最大=![]() ,E(
,E(![]() ,
,![]() );(3)存在,P1(1,
);(3)存在,P1(1,![]() ),P2(1,
),P2(1,![]() ),P3(1,1),P4(1,2).
),P3(1,1),P4(1,2).
【解析】
(1)将点![]() 、
、![]() 的坐标代入函数解析式,列出方程组,通过解方程组求得
的坐标代入函数解析式,列出方程组,通过解方程组求得![]() 、
、![]() 的值即可;利用配方法将函数解析式转化为顶点式,即可得到点
的值即可;利用配方法将函数解析式转化为顶点式,即可得到点![]() 的坐标;
的坐标;
(2)利用待定系数法确定直线![]() 解析式,由函数图象上点的坐标特征求得点
解析式,由函数图象上点的坐标特征求得点![]() 、
、![]() 的坐标,然后根据两点间的距离公式求得
的坐标,然后根据两点间的距离公式求得![]() 长度,结合三角形的面积公式列出函数式,根据二次函数最值的求法求得点
长度,结合三角形的面积公式列出函数式,根据二次函数最值的求法求得点![]() 的横坐标,易得其纵坐标,则点
的横坐标,易得其纵坐标,则点![]() 的坐标迎刃而解了;
的坐标迎刃而解了;
(3)需要分类讨论:点![]() 、
、![]() 、
、![]() 分别为直角顶点,利用勾股定理求得答案.
分别为直角顶点,利用勾股定理求得答案.
解:(1)![]() 抛物线
抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 、
、![]() ,
,
![]()
![]() .
.
解得![]() .
.
![]() ,则
,则![]() ;
;
(2)如图,作![]() 轴交
轴交![]() 于点
于点![]()
![]() ,
,![]() ,
,
![]() 直线
直线![]() 解析式为:
解析式为:![]() .
.
设![]() ,则
,则![]() .
.
![]() .
.
![]() .
.
当![]() 时,S最大
时,S最大![]() .
.
此时,点![]() 的坐标是
的坐标是![]() ,
,![]() ;
;
(3)设![]() ,
,![]() 、
、![]() ,
,
![]() ,
,![]() ,
,![]() .
.
①当![]() 时,
时,![]() ,即
,即![]() .解得
.解得![]() .
.
②当![]() 时,
时,![]() ,即
,即![]() .解得
.解得![]() .
.
③当![]() 时,
时,![]() ,即
,即![]() .解得
.解得![]() 或2.
或2.
综上所述,存在,符合条件的点![]() 的坐标是
的坐标是![]() 或
或![]() 或
或![]() 或
或![]() ,
,



科目:初中数学 来源: 题型:
【题目】在绿化某县城与高速公路的连接路段中,需购买罗汉松、雪松两种树苗共400株,罗汉松树苗每株60元,雪松树苗每株70元.相关资料表明:罗汉松、雪松树苗的成活率分别为70%,90%.
(1)若购买这两种树苗共用去26500元,则罗汉松、雪松树苗各购买多少株?
(2)绿化工程来年一般都要将死树补上新苗,现要使该两种树苗来年共补苗不多于80株,则罗汉松树苗至多购买多少株?
(3)在(2)的条件下,应如何选购树苗,才能使购买树苗的费用最低?请求出最低费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
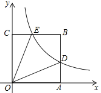
【题目】平面直角坐标系中,正方形OABC如图放置,反比例函数![]() 的图像交AB于点D,交BC于点E,已知A(
的图像交AB于点D,交BC于点E,已知A(![]() ,0),∠DOE=30°,则k的值为( )
,0),∠DOE=30°,则k的值为( )
A.![]() B.
B.![]() C.3D.3
C.3D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
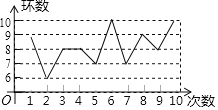
【题目】2019年第七届世界军人运动会(7thCISMMilitaryWorldGames)于2019年10月18日至27日在中国武汉举行,这是中国第一次承办综合性国际军事赛事,也是继北京奥运会后,中国举办的规模最大的国际体育盛会.某射击运动员在一次训练中射击了10次,成绩如图所示.下列结论中不正确的有( )个
①众数是8;②中位数是8;③平均数是8;④方差是1.6.
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 、
、![]() 是两座现代化城市,
是两座现代化城市,![]() 是一个古城遗址,
是一个古城遗址,![]() 城在
城在![]() 城的北偏东
城的北偏东![]() ,在
,在![]() 城的北偏西
城的北偏西![]() ,
,![]() 城在
城在![]() 城的正东方向,且
城的正东方向,且![]() 城与
城与![]() 城相距120千米,现在
城相距120千米,现在![]() 、
、![]() 两城市修建一条笔直的高速公路.
两城市修建一条笔直的高速公路.
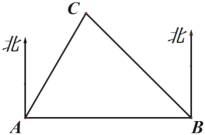
(1)请你计算公路![]() 的长度(结果保留根号);
的长度(结果保留根号);
(2)若以![]() 为圆心,以60千米为半径的圆形区域内为古迹和地下文物保护区,请你分析公路
为圆心,以60千米为半径的圆形区域内为古迹和地下文物保护区,请你分析公路![]() 会不会穿越这个保护区,并说明理由.
会不会穿越这个保护区,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线![]() 的顶点是A(1,3),将OA绕点O逆时针旋转
的顶点是A(1,3),将OA绕点O逆时针旋转![]() 后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.
后得到OB,点B恰好在抛物线上,OB与抛物线的对称轴交于点C.

(1)求抛物线的解析式;
(2)P是线段AC上一动点,且不与点A,C重合,过点P作平行于x轴的直线,与![]() 的边分别交于M,N两点,将
的边分别交于M,N两点,将![]() 以直线MN为对称轴翻折,得到
以直线MN为对称轴翻折,得到![]() .
.
设点P的纵坐标为m.
①当![]() 在
在![]() 内部时,求m的取值范围;
内部时,求m的取值范围;
②是否存在点P,使![]() ,若存在,求出满足m的值;若不存在,请说明理由.
,若存在,求出满足m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是由边长为![]() 的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形
的小正方形构成的网格,每个小正方形的顶点叫做格点.四边形![]() 的顶点在格点上,点
的顶点在格点上,点![]() 是边
是边![]() 边上的一点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
边上的一点.请选择适当的格点,用无刻度的直尺在网格中完成下列画图,保留连线的痕迹,不要求说明理由.
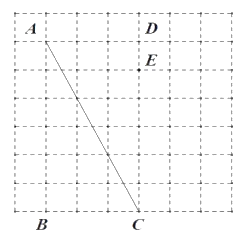
(1)①过![]() 作
作![]() 交
交![]() 边于
边于![]() ;
;
②过![]() 作
作![]() 于
于![]() 点;
点;
③在![]() 上作线段
上作线段![]()
(2)在(1)的条件下,连![]() ,若
,若![]() 为
为![]() 边上的动点,在网格中求作一条线段
边上的动点,在网格中求作一条线段![]() 等于
等于![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com