
【题目】“十房”天然气正在紧张施工中,从2018年1月1日起居民生活用气阶梯价格制度将正式实施,一般生活用气收费标准如下表所示,比如6口以下的户年天然气用量在第二档时,其中350立方米按2.28元/m3收费,超过350立方米的部分按2.5元/m3收费.小冬一家有五口人,他想帮父母计算一下实行阶梯价后,家里天然气费的支出情况.

(1)如果他家2018年全年使用300立方米天然气,那么需要交多少元天然气费?
(2)如果他家2018年全年使用500立方米天然气,那么需要交多少元天然气费?
(3)如果他家2018年需要交1563元天然气费,他家2018年用了多少立方米天然气?
【答案】(1)684;(2)1173;(3)600
【解析】
(1)根据一般生活用气收费标准,可得小冬一家需要交天然气费2.28×300,计算即可;
(2)根据一般生活用气收费标准,可得小冬一家需要交天然气费2.28×350+2.5×(500350),计算即可;
(3)设小冬家2018年用了x立方米天然气.首先判断出小冬家2018年所用天然气超过了500立方米,然后根据他家2018年需要交1563元天然气费建立方程,求解即可.
(1)如果他家2018年全年使用300立方米天然气,那么需要交天然气费2.28×300=684(元);
(2)如果他家2018年全年使用500立方米天然气,那么需要交天然气费
2.28×350+2.5×(500350)=798+375=1173(元);
(3)设小冬家2018年用了x立方米天然气.
∵1563>1173,
∴小冬家2018年所用天然气超过了500立方米.
根据题意得 2.28×350+2.5×(500350)+3.9(x500)=1563,
解得x=600.
答:小冬家2018年用了600立方米天然气.


 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:
我们知道![]() 的几何意义是在数轴上数
的几何意义是在数轴上数![]() 对应的点与原点的距离,即
对应的点与原点的距离,即![]() ,也就是说
,也就是说![]() 表示在数轴上数
表示在数轴上数![]() 与数
与数![]() 对应的点之间的距离,这个结论可以推广为
对应的点之间的距离,这个结论可以推广为![]() 表示数轴上
表示数轴上![]() 与
与![]() 对应点之间的距离.
对应点之间的距离.
例1:已知![]() ,求
,求![]() 的值.
的值.
解:容易看出,在数轴上与原点距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
例2:已知![]() ,求
,求![]() 的值.
的值.
解:在数轴上与![]() 的距离为
的距离为![]() 的点的对应数为
的点的对应数为![]() 和
和![]() ,即
,即![]() 的值为
的值为![]() 和
和![]() .
.
仿照阅读材料的解法,求下列各式中的值.
(1)![]()
(2)![]()
(3)由以上探索猜想:对于任何有理数![]() 是否有最小值?如果有,写出最小值;如果没有,请说明理由.
是否有最小值?如果有,写出最小值;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:知:AM⊥MN,BN⊥MN,垂足分别为M,N,点C是MN上使AC+BC的值最小的点.若AM=3,BN=5,MN=15,则AC+BC=______.
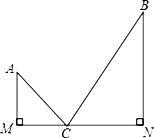
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB⊥BC,BE⊥AC,∠1=∠2,AD=AB,则下列结论不正确的是
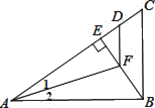
A. BF=DF B. ∠1=∠EFD C. BF>EF D. FD∥BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究,探究过程如下,请补充完整.(1)自变量x的取值范围是全体实数,x与y的几组对应值列表如下:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | 0 |
| 3 | … |
其中,m= .
(2)根据表中数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
(3)观察函数图象,写出两条函数的性质.
(4)进一步探究函数图象发现:
①函数图象与x轴有 个交点,所以对应的方程x2﹣2|x|=0有 个实数根;
②方程x2﹣2|x|=2有 个实数根.

③关于x的方程x2﹣2|x|=a有4个实数根时,a的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是△ABC的角平分线,DE,DF分别是△ABD和△ACD的高,连接EF交AD于G.下列结论:①AD垂直平分EF;②EF垂直平分AD;③AD平分∠EDF;④当∠BAC为60°时,AG=3DG,其中不正确的结论的个数为( )
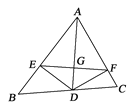
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E为BC边上一点,且AB=AE.
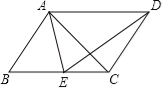
(1)求证:△ABC≌△EAD;
(2)若AE平分∠DAB,∠EAC=25°,求∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
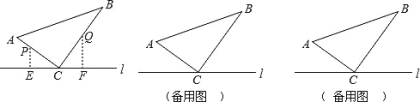
【题目】如图,![]() ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
ABC 中,∠ACB=90°,AC=6cm,BC=8cm,点 P 从 A 点出发沿 A-C-B 路径向终点运动,终点为 B点;点 Q 从 B 点出发沿 B-C-A 路径向终点运动,终点为 A 点,点 P 和 Q 分别以 1cm/s 和 xcm / s 的运动速度 同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过 P 和 Q 作 PE⊥ l 于 E,QF⊥ l 于 F.
(1)如图,当 x 2 时,设点 P 运动时间为 ts ,当点 P 在 AC 上,点 Q 在 BC 上时:
①用含 t 的式子表示 CP 和 CQ,则 CP= cm,CQ= cm;
②当 t 2 时,![]() PEC 与
PEC 与![]() QFC 全等吗?并说明理由;
QFC 全等吗?并说明理由;
(2)请问:当 x 3 时,![]() PEC 与
PEC 与![]() QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
QFC 有没有可能全等?若能,直接写出符合条件的 t 的值;若不能,请说明 理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com