
【题目】已知:如图,在△ABC中,点D,E是边BC上的两点,且AB=BE,AC=CD.
(1)若∠BAC =90°,求∠DAE的度数;
(2)若∠BAC=120°,直接写出∠DAE的度数
(3)设∠BAC=α,∠DAE=β,猜想α与β的之间数量关系(不需证明).

【答案】(1)45°;(2)∠DAE=30°;(3)α+2β=180.
【解析】
(1)由题意得出∠BEA=![]() ,∠CDA =
,∠CDA =![]() ,再在△ADE中
,再在△ADE中
利用内角和等于180°即可.
(2)同(1)理可快速得出答案.
(3)综合(1)(2)可总结出α与β的之间数量关系.
(1)∵AB=BE ,AC=CD
∴∠BEA=![]() ,∠CDA =
,∠CDA =![]()
在△ADE中
∠DAE=180°∠BEA∠CDA=180°![]()
=![]() (∠B+∠C )=
(∠B+∠C )=![]() (180°∠BAC )=
(180°∠BAC )=![]() ×(180°90°)=45°
×(180°90°)=45°
(2)∠DAE=30°
理由:∠DAE=180°∠BEA∠CDA=180°![]()
=![]() (∠B+∠C )=
(∠B+∠C )=![]() (180°∠BAC )= 30°
(180°∠BAC )= 30°
(3)α+2β=180
理由:∠DAE=180°∠BEA∠CDA=180°![]()
=![]() (∠B+∠C )=
(∠B+∠C )=![]() (180°∠BAC )
(180°∠BAC )
∠DAE=![]() (180°∠BAC )
(180°∠BAC )
α+2β=180.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案科目:初中数学 来源: 题型:
【题目】如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
(1)求抛物线的函数关系式;
(2)判断△ABM的形状,并说明理由;
(3)把抛物线与直线y=x的交点称为抛物线的不动点.若将(1)中抛物线平移,使其顶点为(m,2m),当m满足什么条件时,平移后的抛物线总有不动点.

查看答案和解析>>
科目:初中数学 来源: 题型:
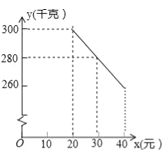
【题目】乌鲁木齐周边多地盛产草莓,今年某水果销售店在草莓销售旺季,以15元/kg 的成本价进50kg有机草莓,销售人员销售发现草莓损坏率为25%;
(1)对于水果店来说完好的草莓实际成本价是多少元/kg?
(2)按照这个实际成本设计销售单价,规定试销期间销售单价不低于成本单价,也不高于每千克40元,经试销发现,销售量y(千克)与销售单价x(元)符合一次函数关系,如图是y与x的函数关系图象,设该水果销售店试销草莓获得的利润为W元,求W的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】推理填空:已知,如图,BCE、AFE是直线,AB∥CD,∠1=∠2,∠3=∠4.求证:AD∥BE.

证明:∵∠4=∠AFD( ),
∵∠3=∠4(已知),
∴∠3=∠ ( ).
∵∠1=∠2(已知),
∴∠1+∠3=∠2+∠AFD( ).
∴∠D=∠ ( ).
∴∠B=∠ ( ).
∴∠________=∠ ( ).
∴AD∥BE( ).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 经过原点O及点A
经过原点O及点A![]() 和点B
和点B![]() .
.
(1)求抛物线的解析式;
(2)如图1,设抛物线的对称轴与x轴交于点C,将直线![]() 沿y轴向下平移n个单位后得到直线l,若直线l经过B点,与y轴交于点D,且与抛物线的对称轴交于点E.若P是抛物线上一点,且PB=PE,求点P的坐标;
沿y轴向下平移n个单位后得到直线l,若直线l经过B点,与y轴交于点D,且与抛物线的对称轴交于点E.若P是抛物线上一点,且PB=PE,求点P的坐标;
(3)如图2,将抛物线向上平移9个单位得到新抛物线,直接写出下列两个问题的答案:
①直线![]() 至少向上平移多少个单位才能与新抛物线有交点?
至少向上平移多少个单位才能与新抛物线有交点?
②新抛物线上的动点Q到直线![]() 的最短距离是多少?
的最短距离是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
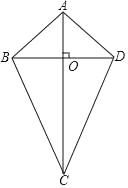
【题目】定义:一条对角线垂直平分另一条对角线的四边形叫做筝形,如图,筝形ABCD的对角线AC、BD相交于点O.且AC垂直平分BD.
(1)请结合图形,写出筝形两种不同类型的性质:性质1: ;性质2: .
(2)若AB∥CD,求证:四边形ABCD为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列资料,解决问题:
定义:在分式中,对于只含有一个字母的分式,当分子的次数小于分母的次数时,我们称之为“真分式”,如:![]() ,这样的分式就是真分式;当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如:
,这样的分式就是真分式;当分子的次数大于或等于分母的次数时,我们称之为“假分式”,如:![]() 这样的分式就是假分式,假分式也可以化为带分式(即:整式与真分式的和的形式).
这样的分式就是假分式,假分式也可以化为带分式(即:整式与真分式的和的形式).
如:![]() .
.
(1)分式![]() 是 (填“真分式”或“假分式”);
是 (填“真分式”或“假分式”);
(2)将假分式![]() 分别化为带分式;
分别化为带分式;
(3)如果分式![]() 的值为整数,求所有符合条件的整数x的值.
的值为整数,求所有符合条件的整数x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com