
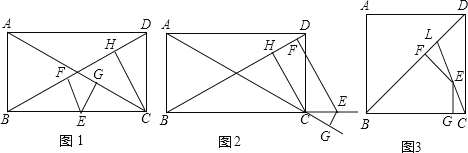
【题目】如图,在矩形ABCD中,点E是BC上的一个动点,过点E作EF⊥BD于点F,EG⊥AC于点G,CH⊥BD于点H,
(1)试证明:CH=EF+EG
(2)若点E在BC的延长线上,如图2,过点E作EF⊥BD于点F,EG⊥AC的延长线于点G,CH⊥BD于点H,则CH、EF、EG之间有怎样的数量关系,直接写出你的猜想;
(3)如图3,BD是正方形ABCD的对角线,L在BD上,且BL=BC,连接CL,点E是CL上一点,EF⊥BD于点F,EG⊥BC于点G,猜想EF、EG、BD之间具有怎样的数量关系,直接写出你的猜想
【答案】(1)见解析; (2)CH=EF-EG;(3)EF+EG= ![]() BD
BD
【解析】
(1)要证明CH=EF+EG,首先要想到能否把线段CH分成两条线段而加以证明,就自然的想到添加辅助线,若作CE⊥NH于N,可得矩形EFHN,很明显只需证明EG=CN,最后根据AAS可求证△EGC≌△CNE得出结论.
(2)过C点作CO⊥EF于O,可得矩形HCOF,因为HC=FO,所以只需证明EO=EG,最后根据AAS可求证△COE≌△CGE得出猜想.
(3)连接BE和AC,交BD于O,由正方形的性质得出AC⊥BD,OA=OB=OC=OD,由三角形面积关系得出S△BCH=S△BCE+S△BHE,证出OC=EG+EF,即可得出结论.
(1)证明:过E点作EN⊥CH于N.
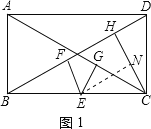
∵EF⊥BD,CH⊥BD,
∴四边形EFHN是矩形.
∴EF=NH,FH∥EN.
∴∠DBC=∠NEC.
∵四边形ABCD是矩形,
∴AC=BD,且互相平分
∴∠DBC=∠ACB
∴∠NEC=∠ACB
∵EG⊥AC,EN⊥CH,
∴∠EGC=∠CNE=90°,
又∵EC=CE,
∴△EGC≌△CNE.
∴EG=CN
∴CH=CN+NH=EG+EF;
(2)解:猜想CH=EF-EG;
过C点作CO⊥EF于O,
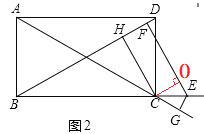
∵EF⊥BD,CH⊥BD,
易得四边形COFH为矩形,
∴CH=OF,
由(1)得∠DBC=∠ACB
又CO∥BD,
∴∠OCE=∠DBC,且∠ECG=∠ACB,
∴∠OCE=∠GCE
又CE=CE,
∴△COE≌△CGE
∴EO=EG
∴CH=EF-EO=EF-EG;
(3)解:EF+EG=![]() BD;
BD;
连接BE和AC,交BD于O,如图3所示:
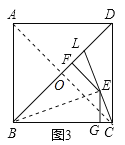
∵四边形ABCD是正方形,
∴AC⊥BD,OA=OB=OC=OD,
∵EF⊥BD于点F,EG⊥BC于点G,
∵S△BCH=S△BCE+S△BHE,
∴![]() BHOC=
BHOC=![]() BCEG+
BCEG+![]() BHEF,
BHEF,
∴OC=EG+EF,
∴EF+EG=![]() BD;
BD;


科目:初中数学 来源: 题型:
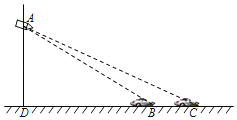
【题目】如图,一辆轿车在经过某路口的感应线B和C处时,悬臂灯杆上的电子警察拍摄到两张照片,两感应线之间距离BC为6m,在感应线B、C两处测得电子警察A的仰角分别为∠ABD=18°,∠ACD=14°.求电子警察安装在悬臂灯杆上的高度AD的长.
(参考数据:sin14°≈0.242,cos14°≈0.97,tan14°≈0.25,sin18°≈0.309,cos18°≈0.951,tan18°≈0.325)
查看答案和解析>>
科目:初中数学 来源: 题型:
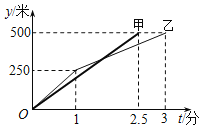
【题目】端午节前夕举行了南通濠河国际龙舟邀请赛,在500米直道竞速赛道上,甲、乙两队所划行的路程y(单位:米)与时间t(单位:分)之间的函数关系式如图所示,根据图中提供的信息,有下列说法:①甲队比乙队提前0.5分到达终点②当划行1分钟时,甲队比乙队落后50米③当划行![]() 分钟时,甲队追上乙队④当甲队追上乙队时,两队划行的路程都是300米其中错误的是( )
分钟时,甲队追上乙队④当甲队追上乙队时,两队划行的路程都是300米其中错误的是( )
A. ①B. ②C. ③D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
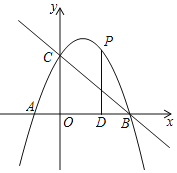
【题目】如图,抛物线![]() 与坐标轴交点分别为
与坐标轴交点分别为![]() ,
,![]() ,
,![]() ,作直线BC.
,作直线BC.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 点P为抛物线上第一象限内一动点,过点P作
点P为抛物线上第一象限内一动点,过点P作![]() 轴于点D,设点P的横坐标为
轴于点D,设点P的横坐标为![]() ,求
,求![]() 的面积S与t的函数关系式;
的面积S与t的函数关系式;
![]() 条件同
条件同![]() ,若
,若![]() 与
与![]() 相似,求点P的坐标.
相似,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数y=kx+4与二次函数y=ax2+c的图像的一个交点坐标为(1,2),另一个交点是该二次函数图像的顶点
(1)求k,a,c的值;
(2)过点A(0,m)(0<m<4)且垂直于y轴的直线与二次函数y=ax2+c的图像相交于B,C两点,点O为坐标原点,记W=OA2+BC2,求W关于m的函数解析式,并求W的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,△ABC的顶点坐标为A(﹣2,3),B(﹣3,2),C(﹣1,1).
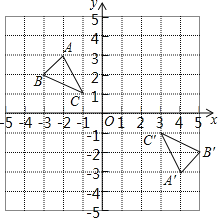
(1)若将△ABC向右平移3个单位长度,再向上平移1个单位长度,请画出平移后的△A1B1C1;
(2)画出△A1B1C1绕原点顺时针旋90°后得到 的△A2B2C2;
(3)若△A′B′C′与△ABC是中心对称图形,则对称中心的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
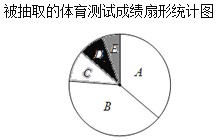
【题目】有一学校为了解九年级学生某次的体育测试成绩,现对这次体育测试成绩进行随机抽样调查,结果统计如下,其中扇形统计图中C等级所在扇形的圆心角为36°.
被抽取的体育测试成绩频数分布表
等级 | 成绩(分) | 频数(人数) |
A | 36<x≤40 | 19 |
B | 32<x≤36 | b |
C | 28<x≤32 | 5 |
D | 24<x≤28 | 4 |
E | 20<x≤24 | 2 |
合计 | a | |
请你根据以上图表提供的信息,解答下列问题:
(1)a= ,b= ;
(2)A等级的频率是 ;
(3)在扇形统计图中,B等级所对应的圆心角是 度;
(4)已知该校九年级共有780学生,估计成绩(分)在32<x≤36之间的学生约有 人.
查看答案和解析>>
科目:初中数学 来源: 题型:
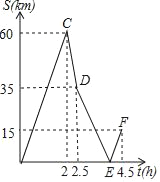
【题目】A、B两地相距150km,甲、乙两人先后从A地出发向B地行驶,甲骑摩托车匀速行驶,乙开汽车且途中速度只改变一次,如图表示的是甲、乙两人之间的距离S关于时间t的函数图象(点F的实际意义是乙开汽车到达B地),请根据图象解答下列问题:
(1)求出甲的速度;
(2)求出乙前后两次的速度,并求出点E的坐标;
(3)当甲、乙两人相距10km时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,延长BG交CD于F点,若CF=1,FD=2,则BC的长为【 】

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com