
【题目】如图,等边△ABC中,AB=2,点D是以A为圆心,半径为1的圆上一动点,连接CD,取CD的中点E,连接BE,则线段BE的最大值与最小值之和为____.

【答案】![]()
【解析】
取点D的特殊位置:当点D与点F重合时,当点D在CA延长线与圆A的交点时,当CD与圆A相切时,确定FE的长度都是0.5,从而得到点E的运动轨迹是以点F为圆心,0.5为半径的圆上运动,故而得到线段BE的最大值与最小值,由此得到答案.
∵△ABC为等边三角形,AB=2,
∴AC=AB=2,
设AC交圆A于点F,
∵点D是以A为圆心,半径为1的圆上一动点,
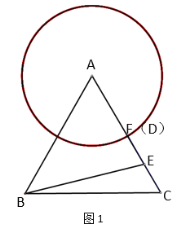
∴当点D与点F重合时,如图1,FE=0.5,
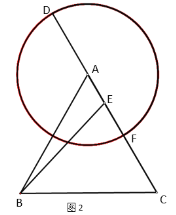
当点D在CA延长线与圆A的交点时,如图2,FE=0.5,
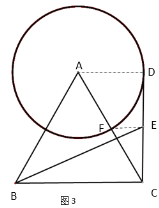
当CD与圆A相切时,FE=0.5,
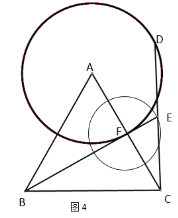
故点E在以点F为圆心,0.5为半径的圆上运动,
当点B、F、E三点共线时,线段BE有最大值和最小值,如图4:
∵AF=1,AC=2,
∴FC=1,
∴点F是AC的中点,
∵△ABC是等边三角形,
∴BF⊥AC,
∴BF=![]() ,
,
线段BE的最大值=![]() ,最小值=
,最小值=![]() ,
,
∴线段BE的最大值与最小值之和为![]() ,
,
故答案为:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图①,点G是等边三角形AOB的外心,点A在第一象限,点B坐标为(4,0),连结OG.抛物线y=ax(x﹣2)+1+![]() 的顶点为P.
的顶点为P.
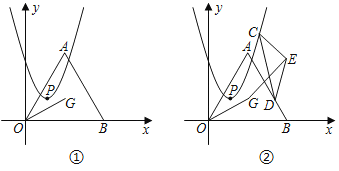
(1)直接写出点A的坐标与抛物线的对称轴;
(2)连结OP,求当∠AOG=2∠AOP时a的值.
(3)如图②,若抛物线开口向上,点C,D分别为抛物线和线段AB上的动点,以CD为底边构造顶角为120°的等腰三角形CDE(点C,D,E成逆时针顺序),连结GE.
①点Q在x轴上,当四边形GDQO为平行四边形时,求GQ的值;
②当GE的最小值为1时,求抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,E、F分别为BC、CD的中点,连接AE,BF交于点G,将△BCF沿BF对折,得到△BPF,延长FP交BA延长线于点Q,下列结论正确的个数是( )
①AE=BF;②AE⊥BF;③sin∠BQP=![]() ;④S四边形ECFG=2S△BGE.
;④S四边形ECFG=2S△BGE.
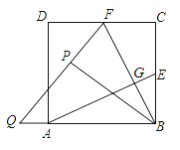
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系xOy中,二次函数y=mx 2 +2mx-4(m≠0)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,△ABC的面积为12.
(1)求这个二次函数的解析式;
(2)点D的坐标为(-2,1),点P在二次函数的图象上,∠ADP为锐角,且tan∠ADP=2,求出点P的横坐标;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明设计了一个摸球实验:在一个不透明的箱子里放入4个相同的小球,球上分别标有数字0,10,20和30,然后从箱子里先后摸出两个小球(第一次摸出后不放回).
(1)摸出的两个小球上所标的数字之和至少为 ,最多为 ;
(2)请你用画树状图或列表的方法,求出摸出的两个小球上所标的数字之和不低于30的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:每个内角都相等的八边形叫做等角八边形.容易知道,等角八边形的内角都等于135°.下面,我们来研究它的一些性质与判定:
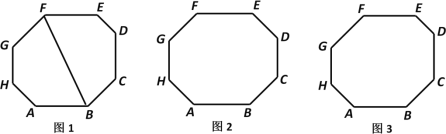
(1)如图1,等角八边形ABCDEFGH中,连结BF.
①请直接写出∠ABF+∠GFB的度数.
②求证:AB∥EF.
③我们把AB与EF称为八边形的一组正对边.由②同理可得:BC与FG,CD与GH,DE与HA这三组正对边也分别平行.请模仿平行四边形性质的学习经验,用一句话概括等角八边形的这一性质.
(2)如图2,等角八边形ABCDEFGH中,如果有AB=EF,BC=FG,则其余两组正对边CD与GH,DE与HA分别相等吗?证明你的结论.
(3)如图3,八边形ABCDEFGH中,若四组正对边分别平行,则显然有∠A=∠E,∠B=∠F,∠C=∠G,∠D=∠H.请探究:该八边形至少需要已知几个内角为135°,才能保证它一定是等角八边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”,某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题做法全校学生中进行了抽样调查,根据调查结果绘制城如图所示的两个不完整的统计图,请结合图中信息解决下列问题:
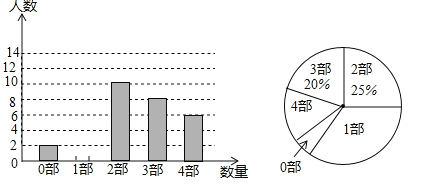
(1)本次调查所得数据的众数是 部,中位数是 部,扇形统计图中“1部”所在扇形的圆心角为 度.
(2)请将条形统计图补充完整;
(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,则他们选中同一名著的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了提高学生的阅读能力,我市某校开展了“读好书,助成长”的活动,并计划购置一批图书,购书前,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,请根据统计图回答下列问题:
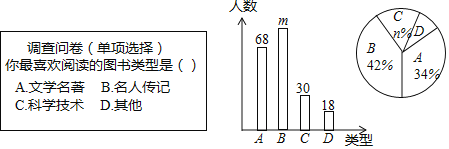
(1)本次调查共抽取了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有3600名学生,请你估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校将举办读书知识竞赛,九年级1班要在本班3名优胜者(2男1女)中随机选送2人参赛,请用列表或画树状图的方法求被选送的两名参赛者为一男一女的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com