练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】按要求完成下列视图问题：

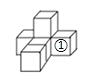
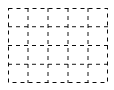
    （1）如图（1），它是由6个同样大小的正方体摆成的几何体，将正方体①移走后，新几何体从三个方向看到的图形与原几何体从三个方向看到的图形相比，从 方向看到的形状图没有发生改变？

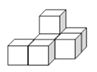
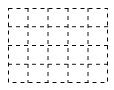
    （2）如图（2），请你在右侧虚线网格图a中画出该几何体从上面看到的形状图

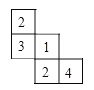
    （3）如图（3），它是由几个小立方块组成从上面看到的形状图，小正方形上的数字表示该位置上的正方体的个数，请你在右侧建线网格图b中面出该几何体从正面看到的形状图．

    【答案】（1）左

    （2）见详解；

    （3）见详解.

    【解析】

    （1）利用几何体的形状，结合三视图可知左视图没有发生改变；

    （2）利用几何体的形状，结合从上面看到的形状可画出俯视图；

    （3）利用小立方体的个数结合几何体，可画出主视图.

    （1）利用几何体的形状，结合三视图可知左视图没有发生改变

    故答案为左

    （2）如图

    （3）如图

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】观察下列等式：

    （1）；

    （2）；

    （3）；

    （4）；

    ……

    根据上述等式的规律，解答下列问题：

    （1）写出第5个等式：________________；

    （2）写出第个等式：__________________（用含有的代数式表示）；

    （3）应用你发现的规律，计算：。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】探索代数式a2 2ab+b2与代数式(a b)2的关系．

    （1）当a=1，b=2时分别计算两个代数式的值．

    （2）当a=3，b= 2时分别计算两个代数式的值．

    （3）你发现了什么规律？

    （4）利用你发现的规律计算：732 2×73×67+672.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，锐角△ABC内接于⊙O，若⊙O的半径为6，sinA=，求BC的长．

    【答案】BC=8．

    【解析】试题分析：通过作辅助线构成直角三角形，再利用三角函数知识进行求解．

    试题解析：作⊙O的直径CD，连接BD，则CD=2×6=12.

    ∵

    ∴

    ∴

    点睛：直径所对的圆周角是直角.

    【题型】解答题
    【结束】
    22

    【题目】如图，一次函数y=k1x+b与反比例函数y=的图象交于A（2，m），B（n，﹣2）两点．过点B作BC⊥x轴，垂足为C，且S△ABC=5．

    （1）求一次函数与反比例函数的解析式；

    （2）根据所给条件，请直接写出不等式k1x+b＞的解集；

    （3）若P（p，y1），Q（﹣2，y2）是函数y=图象上的两点，且y1≥y2，求实数p的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

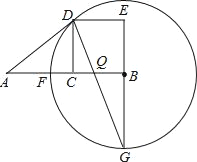
    【题目】设C为线段AB的中点，四边形BCDE是以BC为一边的正方形．以B为圆心，BD长为半径的⊙B与AB相交于F点，延长EB交⊙B于G点，连接DG交于AB于Q点，连接AD．

    求证：（1）AD是⊙B的切线；（2）AD=AQ；（3）BC2=CFEG．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，在△ABC中，∠BAC=90°，AB=AC，在△ABC内部作△CED，使∠CED=90°，E在BC上，D在AC上，分别以AB，AD为邻边作平行四边形ABFD，连接AF、AE、EF．

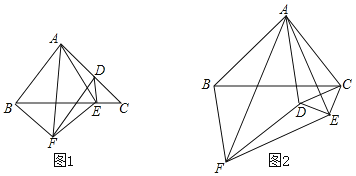
    （1）证明：AE=EF；

    （2）判断线段AF，AE的数量关系，并证明你的结论；

    （3）在图（1）的基础上，将△CED绕点C逆时针旋转，请判断（2）问中的结论是否成立？若成立，结合图（2）写出证明过程；若不成立，请说明理由

    查看答案和解析>>

    科目：初中数学 来源： 题型：

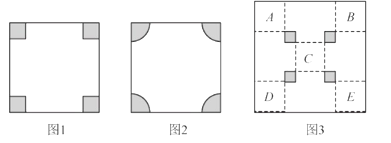
    【题目】（1）探索：如图1，在边长为的正方形纸片的4个角都剪去1个边长是的正方形.试用含的式子表示纸片剩余部分的面积为_______________________；

    （2）变式：如图2，在边长为的正方形纸片的4个角都剪去一个相同的扇形，扇形的半径为，用表示纸片剩余部分面积为______________________，剩余部分图形的周长为_____________________；

    （3）拓展：世博会中国国家馆模型的平面图如图3所示，其外框是一个大正方形，中间四个全等的小正方形（阴影部分）是支撑展馆的核心筒，标记字母的五个全等的正方形是展厅，展厅的边长为，已知核心筒的边长比展厅的边长的一半多1米，用含有的式子表示外框的边长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

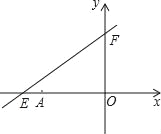
    【题目】如图，直线y=kx+6分别与x轴、y轴交于点E，F，已知点E的坐标为（﹣8，0），点A的坐标为（﹣6，0）．

    （1）求k的值；

    （2）若点P（x，y）是该直线上的一个动点，且在第二象限内运动，试写出△OPA的面积S关于x的函数解析式，并写出自变量x的取值范围．

    （3）探究：当点P运动到什么位置时，△OPA的面积为，并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某市提倡“诵读中华经典，营造书香校园”的良好诵读氛围，促进校园文化建设，进而培养学生的良好诵读习惯，使经典之风浸漫校园．某中学为了了解学生每周在校经典诵读时间，在本校随机抽取了若干名学生进行调查，并依据调查结果绘制了以下不完整的统计图表，请根据图表信息解答下列问题：

    时间（小时）

    频数（人数）

    频率

    2≤t＜3

    4

    0.1

    3≤t＜4

    10

    0.25

    4≤t＜5

    a

    0.15

    5≤t＜6

    8

    b

    6≤t＜7

    12

    0.3

    合计

    40

    1

    （1）表中的a＝　 　，b＝　 　；

    （2）请将频数分布直方图补全；

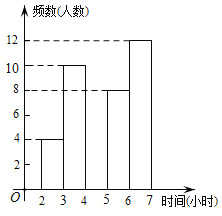
    （3）若该校共有1200名学生，试估计全校每周在校参加经典诵读时间至少有4小时的学生约为多少名？

    查看答案和解析>>

    同步练习册答案