
【题目】目前节能灯在城市已基本普及,今年山东省面向县级及农村地区推广,为响应号召,某商场计划购进甲,乙两种节能灯共![]() 只,这两种节能灯的进价、售价如下表:
只,这两种节能灯的进价、售价如下表:
进价(元/只) | 售价(元/只) | |
甲型 |
|
|
乙型 |
|
|
(1)如何进货,进货款恰好为![]() 元?
元?
(2)设商场购进甲种节能灯![]() 只,求出商场销售完节能灯时总利润
只,求出商场销售完节能灯时总利润![]() 与购进甲种节能灯
与购进甲种节能灯![]() 之间的函数关系式;
之间的函数关系式;
(3)如何进货,商场销售完节能灯时获利最多且不超过进货价的![]() ,此时利润为多少元?
,此时利润为多少元?
【答案】(1)乙型节能灯为800; (2)![]()
![]() ; (3)购进乙型节能灯
; (3)购进乙型节能灯![]() 只时的最大利润为
只时的最大利润为![]() 元.
元.
【解析】
(1)设商场购进甲型节能灯x只,则购进乙型节能灯(1200x)只,根据两种节能灯的总价为46000元建立方程求出其解即可;
(2)设商场应购进甲开型节能灯x只,根据题意列出函数解析式即可;
(3)根据(2)的结论解答即可.
(1)设商场应购进甲型节能灯![]() 只,则乙型节能灯为
只,则乙型节能灯为![]() 只.
只.
根据题意得,![]() ,
,
解得 ![]() ,
,
所以乙型节能灯为:![]() ;
;
(2)设商场应购进甲型节能灯![]() 只,商场销售完这批节能灯可获利
只,商场销售完这批节能灯可获利![]() 元.
元.
根据题意得,![]()
![]()
![]() ;
;
(3)![]() 商场销售完节能灯时获利最多且不超过进货价的
商场销售完节能灯时获利最多且不超过进货价的![]() ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() 随
随![]() 的增大而减小,
的增大而减小,
![]() 时,
时,![]() 最大
最大![]() 元.
元.
![]() 商场购进甲型节能灯
商场购进甲型节能灯![]() 只,
只,
购进乙型节能灯![]() 只时的最大利润为
只时的最大利润为![]() 元.
元.


 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:
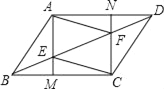
【题目】如图,已知平行四边形ABCD,过A点作AM⊥BC于M,交BD于E,过C点作CN⊥AD于N,交BD于F,连接AF、CE.
(1)求证:四边形AECF为平行四边形;
(2)当AECF为菱形,M点为BC的中点时,求AB:AE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E、F分别是边AB、CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于O点,且BE=BF,∠BEF=2∠BAC。

(1)求证:OE=OF;
(2)若BC=![]() ,求AB的长。
,求AB的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级6班的一个互助学习小组组长收集并整理了组员们讨论如下问题时所需的条件:如图所示,在四边形ABCD中,点E、F分别在边BC、AD上,____,求证:四边形AECF是平行四边形. 你能在横线上填上最少且简捷的条件使结论成立吗?
条件分别是:①BE=DF;②∠B=∠D;③BAE=∠DCF;④四边形ABCD是平行四边形.
其中A、B、C、D四位同学所填条件符合题目要求的是( )
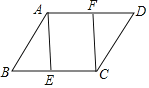
A. ①②③④B. ①②③C. ①④D. ④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】点O为直线AB上一点,过点O作射线OC,使∠BOC=65°,将一直角三角板的直角顶点放在点O处.
(1)如图①,将三角板MON的一边ON与射线OB重合时,则∠MOC= ;
(2)如图②,将三角板MON绕点O逆时针旋转一定角度,此时OC是∠MOB的角平分线,求旋转角∠BON和∠CON的度数;
(3)将三角板MON绕点O逆时针旋转至图③时,∠NOC=![]() ∠AOM,求∠NOB的度数.
∠AOM,求∠NOB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(1,0),B(0,3),将Rt△AOB绕点O逆时针旋转90°,得到Rt△COD,CD的延长线,交AB于点E,连接BC,二次函数![]() 的图象过点A、B、C.
的图象过点A、B、C.
(1)求二次函数的解析式;
(2)点P是线段BC上方抛物线上的一个动点,当∠PBC=75°时,求点P的坐标;
(3)设抛物线的对称轴与x轴交于点F,在抛物线的对称轴上,是否存在一点Q,使得以点Q、O、F为顶点的三角形,与△BDE相似?若存在,请求出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】函数 yl= x ( x ≥0 ) , ![]() ( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3
( x > 0 )的图象如图所示,则结论: ① 两函数图象的交点A的坐标为(3 ,3 ) ② 当 x > 3 ![]() 时, ③ 当 x =1时, BC = 8
时, ③ 当 x =1时, BC = 8
④ 当 x 逐渐增大时, yl 随着 x 的增大而增大,y2随着 x 的增大而减小.其中正确结论的序号是_ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在艺术节中组织中小学校文艺汇演,甲、乙两所学校共92名学生![]() 其中甲校学生多于乙校学生,且甲校学生不足90名
其中甲校学生多于乙校学生,且甲校学生不足90名![]() ,现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
,现准备统一购买服装参加演出,下表是某服装厂给出的演出服装价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套及以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两所学校单独购买服装,一共应付5000元
(1)甲、乙两校各有多少名学生准备参加汇演?
(2)如果甲、乙两校联合起来购买服装,那么比各自购买服装共可以节省多少钱?
(3)如果甲校有10名学生被调去参加书法绘画比赛不能参加演出,请你为两校设计购买服装方案,并说明哪一种最省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】怡然美食店的A、B两种菜品,每份成本均为14元,售价分别为20元、18元,这两种菜品每天的营业额共为1120元,总利润为280元.
(1)该店每天卖出这两种菜品共多少份?
(2)该店为了增加利润,准备降低A种菜品的售价,同时提高B种菜品的售价,售卖时发现,A种菜品售价每降0.5元可多卖1份;B种菜品售价每提高0.5元就少卖1份,如果这两种菜品每天销售总份数不变,那么这两种菜品一天的总利润最多是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com