
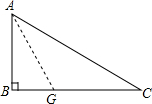
 如图,已知直角△ABC中,∠B=90°,AB=6cm,BC=8cm,把AB沿AG折叠,使B点恰好落在AC上,求折痕AG的长.
如图,已知直角△ABC中,∠B=90°,AB=6cm,BC=8cm,把AB沿AG折叠,使B点恰好落在AC上,求折痕AG的长. 分析 由勾股定理,可得AC的长,根据折叠得到的图形与原图形是全等图形,可得对应的边相等,由勾股定理,可得BG的长,再由勾股定理即可得出结果.
解答 解:设BG=x,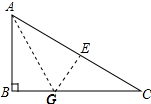
在Rt△ABC中,由勾股定理得:
AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10,
折叠纸片使AB边与AC边重合,B点落在点E上,如图所示:
AE=AB=6,BG=GE=x,
EC=AC-AE=10-6=4,
GC=BC-BG=8-x,
在Rt△CEG中,由勾股定理得:
GE2+CE2=GC2
x2+42=(8-x)2
解得:x=3,即BG=3,
在Rt△ABG中,由勾股定理得:
AG=$\sqrt{A{B}^{2}+B{G}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$.
即折痕AG的长为3$\sqrt{5}$.
点评 本题考查了翻折变换、勾股定理、解方程等知识;熟练掌握翻折变换的性质,由勾股定理求出BG是解决问题的关键.


 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,B在AE上,C在BG上,四边形ABCD和四边形BEFG都是正方形,连结AG和EC.
如图,B在AE上,C在BG上,四边形ABCD和四边形BEFG都是正方形,连结AG和EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
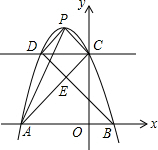 已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,0),B(1,0),C(0,3)三点.
已知抛物线y=ax2+bx+c(a≠0)经过点A(-3,0),B(1,0),C(0,3)三点.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com