
【题目】如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.

【答案】(1)一次函数的解析式是y=-![]() x+
x+![]() ;(2)S△ABC=
;(2)S△ABC=![]() ;(3)x≥-1.
;(3)x≥-1.
【解析】试题分析:利用代入法求出点A的坐标,然后根据待定系数法求出一次函数的解析式;
(2)根据图像求出交点C的坐标,然后可求三角形的面积;
(3)根据图像的位置求出不等式的解集.
试题解析:解:(1)把A(a,2)代入y=-2x中,得-2a=2,∴a=-1,∴A(-1,2),把A(-1,2)、B(2,0)代入y=kx+b中得![]() ,∴k=-
,∴k=-![]() ,b=
,b=![]() ,∴一次函数的解析式是y=-
,∴一次函数的解析式是y=-![]() x+
x+![]() ;
;
(2)设直线AB与y轴交于点C,则C(0,![]() ),∴S△ABC=
),∴S△ABC=![]() ×
×![]() ×1=
×1=![]() ;
;
(3)不等式(k+2)x+b≥0可以变形为kx+b≥-2x,结合图象得到解集为:x≥-1.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
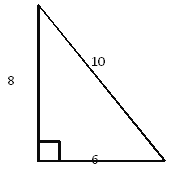
【题目】如图,已知一个边长分别为6、8、10的直角三角形,请设计出一个有一条边长为8的直角三角形,使这两个直角三角形能够拼成一个等腰三角形.
(1)画出4种不同拼法(周长不等)的等腰三角形;
(2)分别求出4种不同拼法的等腰三角形的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
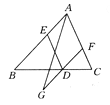
【题目】如图所示,已知D,E,F分别在△ABC的边BC,AB,AC上,且DE∥AF,DE=AF,将FD延长至G,使FG=2DF,连接AG,则ED,AG互相平分吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下四种沿AB折叠的方法中,不一定能判定纸带两条边线a,b互相平行的是( )
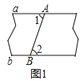


A. 如图1,展开后测得∠1=∠2
B. 如图2,展开后测得∠1=∠2且∠3=∠4
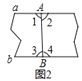
C. 如图3,测得∠1=∠2
D. 如图4,展开后再沿CD折叠,两条折痕的交点为O,测得OA=OB,OC=OD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,我们曾经研究过n×n的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2 . 但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道0×1+1×2+2×3+…+(n﹣l)×n
= ![]() n(n+1)(n﹣1)时,我们可以这样做:
n(n+1)(n﹣1)时,我们可以这样做:
(1)观察并猜想:
12+22=(1+0)×1+(1+1)×2=l+0×1+2+1×2=(1+2)+(0×1+1×2)
12+22+32=(1+0)×1+(1+1)×2+(l+2)×3
=1+0×1+2+1×2+3+2×3
=(1+2+3)+(0×1+1×2+2×3)
12+22+32+42=(1+0)×1+(1+1)×2+(l+2)×3+
=1+0×1+2+1×2+3+2×3+
=(1+2+3+4)+()
…
(2)归纳结论:
12+22+32+…+n2=(1+0)×1+(1+1)×2+(1+2)×3+…[1+(n﹣l)]n
=1+0×1+2+1×2+3+2×3+…+n+(n﹣1)×n
=()+[]
=+
= ![]() ×
×
(3)实践应用:
通过以上探究过程,我们就可以算出当n为100时,正方形网格中正方形的总个数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
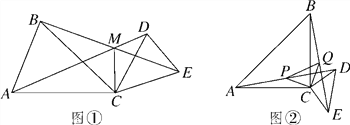
【题目】如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,最适合采用普查方式的是( )
A. 对太原市民知晓“中国梦”内涵情况的调查
B. 对全班同学1分钟仰卧起坐成绩的调查
C. 对2018年央视春节联欢晚会收视率的调查
D. 对2017年全国快递包裹产生的包装垃圾数量的调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图E在△ABC的边AC上,且∠AEB=∠ABC.
⑴求证:∠ABE=∠C;
⑵若∠BAE的平分线AF交BE于F,FD∥BC交AC于D,设AB=5,AC=8,求DC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com