
【题目】同学们,我们曾经研究过n×n的正方形网格,得到了网格中正方形的总数的表达式为12+22+32+…+n2 . 但n为100时,应如何计算正方形的具体个数呢?下面我们就一起来探究并解决这个问题.首先,通过探究我们已经知道0×1+1×2+2×3+…+(n﹣l)×n
= ![]() n(n+1)(n﹣1)时,我们可以这样做:
n(n+1)(n﹣1)时,我们可以这样做:
(1)观察并猜想:
12+22=(1+0)×1+(1+1)×2=l+0×1+2+1×2=(1+2)+(0×1+1×2)
12+22+32=(1+0)×1+(1+1)×2+(l+2)×3
=1+0×1+2+1×2+3+2×3
=(1+2+3)+(0×1+1×2+2×3)
12+22+32+42=(1+0)×1+(1+1)×2+(l+2)×3+
=1+0×1+2+1×2+3+2×3+
=(1+2+3+4)+()
…
(2)归纳结论:
12+22+32+…+n2=(1+0)×1+(1+1)×2+(1+2)×3+…[1+(n﹣l)]n
=1+0×1+2+1×2+3+2×3+…+n+(n﹣1)×n
=()+[]
=+
= ![]() ×
×
(3)实践应用:
通过以上探究过程,我们就可以算出当n为100时,正方形网格中正方形的总个数是 .
科目:初中数学 来源: 题型:
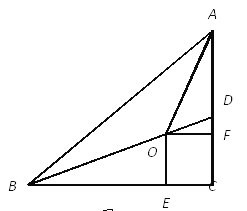
【题目】如图,在Rt△ABC中,∠C=90,BD是△ABC的角平分线,点O在BD上,分别过点O作OE⊥BC,OF⊥AC,垂足为E,F,且OE=OF.
(1)求证:点O在∠BAC的平分线上;
(2)若AC=5,BC=12,求OE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列运算正确的是( )
A. x6+x6=2x12B. a2a4﹣(﹣a3)2=0
C. (x﹣y)2=x2﹣2xy﹣y2D. (a+b)(b﹣a)=a2+b2
查看答案和解析>>
科目:初中数学 来源: 题型:
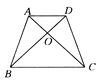
【题目】如图所示,在四边形ABCD中,已知AB与 CD不平行,∠ABD=∠ACD,请你添加一个条件:______ ,使的加上这个条件后能够推出AD∥BC ,且AB=CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
A.1cm,2cm,2cmB.1cm,2cm,4cm
C.2cm,3cm,5cmD.5cm,6cm,12cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com