
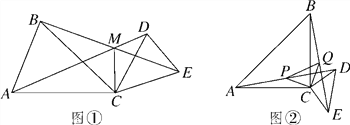
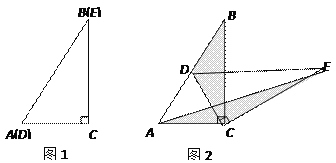
【题目】如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.
【答案】(1)证明见解析;(2)∠AMB=α;(3)△CPQ为等腰直角三角形,证明见解析.
【解析】试题分析:(1)由CA=CB,CD=CE,∠ACB=∠DCE=α,利用SAS即可判定△ACD≌△BCE;
(2)根据△ACD≌△BCE,得出∠CAD=∠CBE,再根据∠AFC=∠BFH,即可得到∠AMB=∠ACB=α;
(3)先根据SAS判定△ACP≌△BCQ,再根据全等三角形的性质,得出CP=CQ,∠ACP=∠BCQ,最后根据∠ACB=90°即可得到∠PCQ=90°,进而得到△PCQ为等腰直角三角形.
试题解析:(1)证明:如图①,∵∠ACB=∠DCE=α,
∴∠ACD=∠BCE.在△ACD和△BCE中,
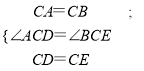
∴△ACD≌△BCE(SAS),
∴BE=AD.
(2)解:如图①,∵△ACD≌△BCE,
∴∠CAD=∠CBE.
∵∠BAC+∠ABC=180°-α,
∴∠BAM+∠ABM=180°-α,
∴∠AMB=180°-(180°-α)=α.
(3)解:△CPQ为等腰直角三角形.
证明:如图②,由(1)可得,BE=AD.
∵AD,BE的中点分别为点P,Q,
∴AP=BQ.
∵△ACD≌△BCE,
∴∠CAP=∠CBQ.在△ACP和△BCQ中,
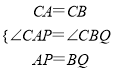
∴△ACP≌△BCQ(SAS),
∴CP=CQ且∠ACP=∠BCQ.
又∵∠ACP+∠PCB=90°,
∴∠BCQ+∠PCB=90°,
∴∠PCQ=90°,
∴△CPQ为等腰直角三角形.


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】方图,其中产品净重的范围是[96,106](即96≤净重≤106),样本数据分组为[96,98)(即96≤净重<98)以下类似,[98,100),[100,102),[102,104),[104,106],已知样本中产品净重小于100克的个数是36,则样本中净重大于或等于98克并且小于104克的产品的个数是( )
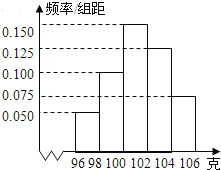
A. 90 B. 75 C. 60 D. 45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点.将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A、D重合,连接BE、EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想. 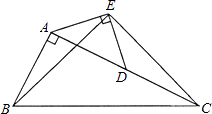
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在直角梯形ABCD中,AD∥BC,∠B=90°,AD=24 ㎝,BC=26㎝,动点P从点A开始沿AD边以每秒1㎝的速度向D点运动,动点Q从点C开始沿CB边以每秒3㎝的速度向B运动,P,Q分别从A,C同时出发,当其中一点到达端点时,另一点也随之停止运动,设运动时间为t s.
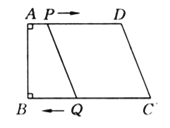
(1)t为何值时,四边形PQCD为平行四边形?
(2)t为何值时,四边形PQCD为等腰梯形?
(3)t为何值时,四边形ABQP为矩形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-2x与直线y=kx+b相交于点A(a,2),并且直线y=kx+b经过x轴上点B(2,0).
(1)求直线y=kx+b的解析式;
(2)求两条直线与y轴围成的三角形面积;
(3)直接写出不等式(k+2)x+b≥0的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D是BC上任意一点,过D分别向AB,AC引垂线,垂足分别为E,F,CG是AB边上的高.
(1)当D点在BC的什么位置时,DE=DF?请说明理由.
(2)DE,DF,CG的长之间存在着怎样的等量关系?并说明理由.
(3)若D在底边BC的延长线上,(2)中的结论还成立吗?若不成立,又存在怎样的关系?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米.假设她们的
眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)( )
≈1.732)( )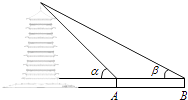
A.36.21米
B.37.71米
C.40.98米
D.42.48米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将两个完全相同的三角形纸片ABC和DEC重合放置,其中∠C=90°,∠B=∠E=30°.
(1)操作发现
如图2,固定△ABC,使△DEC绕点C旋转,当点D恰好落在AB边上时,填空:
①线段DE与AC的位置关系是_________;
②设△BDC的面积为S1,△AEC的面积为S2,则S1与S2的数量关系是____________.

(2)猜想论证
当△DEC绕点C旋转到图3所示的位置时,小明猜想(1)中S1与S2的数量关系仍然成立,并尝试分别作出了△BDC和△AEC中BC、CE边上的高,请你证明小明的猜想.
(3)拓展探究
已知∠ABC=60°,点D是其角平分线上一点,BD=CD=4,DE//AB交BC于点E(如图4).若在射线BA上存在点F,使![]() ,请直接写出相应的BF的长.
,请直接写出相应的BF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把点A(3,5)向下平移3个单位长度,再向左平移2个单位长度后,得对应点A1的坐标是( )
A.(1,2)B.(2,1)C.(﹣1,2)D.(﹣1,﹣2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com