
 “龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场,图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程,求兔子在途中多少米处追上乌龟?
“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结并反思后,和乌龟约定再赛一场,图中的函数图象刻画了“龟兔再次赛跑”的故事,x表示乌龟从起点出发所行的时间,y1表示乌龟所行的路程,y2表示兔子所行的路程,求兔子在途中多少米处追上乌龟?
|
|


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案科目:初中数学 来源: 题型:
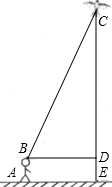 八年级三班小明和小亮同学学习了“勾股定理”之后,为了测得下图风筝CE的高度,他们进行了如下操作:
八年级三班小明和小亮同学学习了“勾股定理”之后,为了测得下图风筝CE的高度,他们进行了如下操作:查看答案和解析>>
科目:初中数学 来源: 题型:
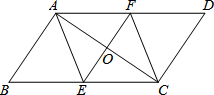 如图,在?ABCD中,EF垂直平分AC交BC于E,交AD于F.
如图,在?ABCD中,EF垂直平分AC交BC于E,交AD于F.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面直角坐标系中,抛物线y1=
如图,在平面直角坐标系中,抛物线y1=| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 3 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在平面内有A、B、C三点.
如图,在平面内有A、B、C三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com