
分析 根据价格上涨或下降时销售量的不同,分60≤x≤90、x>90两种情况,根据:每天获得的利润=每个商品的利润×每天的销售量列出函数表达式,配方分别求出其最大值,比较大小后可得.
解答 解:设该商品的售价定为x元/个时,每天获得的利润为W元,根据题意,
当60≤x≤90时,
W=(x-60)[100+10(90-x)]=-10x2+1600x-60000=-10(x-80)2+4000,
∴当x=80时,W取得最大值,最大值为4000;
当x>90时,
W=(x-60)[100-2(x-90)]=-2x2+400x-16800=-2(x-100)2+3200,
当x=100时,W取得最大值,最大值为3200;
综上,当x=80时,W取得最大值4000元,
答:该商品的定价为80元/个时专卖店每天可获得最大利润4000元.
点评 本题考查了二次函数的应用,根据价格上涨或下降时销售量的不同分类讨论是前提,解题的关键是根据题目中的等量关系列出函数关系式.


科目:初中数学 来源: 题型:选择题
| A. | 2-$\sqrt{3}$,1 | B. | -6-$\sqrt{3}$,15-8$\sqrt{3}$ | C. | $\sqrt{3}$-2,-1 | D. | 2+$\sqrt{3}$,7+4$\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
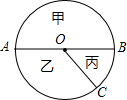 如图,AB是圆的直径,OC是圆的半径,扇形乙与扇形丙的面积比为2:1
如图,AB是圆的直径,OC是圆的半径,扇形乙与扇形丙的面积比为2:1查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com