
分析 分别计算两个二次根式混合运算的最后结果即可得知.
解答 解:不等于,
∵2$\sqrt{2}$÷(4$\sqrt{2}$-3$\sqrt{6}$)=2$\sqrt{2}$×$\frac{1}{4\sqrt{2}-3\sqrt{6}}$
=2$\sqrt{2}$×$\frac{4\sqrt{2}+3\sqrt{6}}{(4\sqrt{2}-3\sqrt{6})(4\sqrt{2}+3\sqrt{6})}$
=2$\sqrt{2}$×$\frac{4\sqrt{2}+3\sqrt{6}}{32-54}$
=-$\frac{16+12\sqrt{3}}{22}$,
2$\sqrt{2}$÷4$\sqrt{2}$-2$\sqrt{2}$÷3$\sqrt{6}$=$\frac{1}{2}-\frac{2\sqrt{3}}{9}$,
∴2$\sqrt{2}$÷(4$\sqrt{2}$-3$\sqrt{6}$)不等于2$\sqrt{2}$÷4$\sqrt{2}$-2$\sqrt{2}$÷3$\sqrt{6}$.
点评 本题考查的是二次根式的混合运算,解决此题的关键是不能与乘法的分配律混淆,熟练掌握二次根式混合运算的顺序、步骤是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
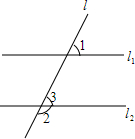 如图,若∠1+∠2=180°,则l1∥l2,试说明理由(填空).
如图,若∠1+∠2=180°,则l1∥l2,试说明理由(填空).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com