
【题目】在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为16cm的等腰直角三角形.
(1)在等腰直角三角形ABC纸片中,以C为圆心,剪出一个面积最大的扇形(要求:尺规作图,保留作图痕迹,不写作法);
(2)请求出所制作圆锥底面的半径长.

 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.
(1)求A、B、C的坐标;
(2)点M为线段AB上一点(点M不与点A、B重合),过点M作x轴的垂线,与直线AC交于点E,与抛物线交于点P,过点P作PQ∥AB交抛物线于点Q,过点Q作QN⊥x轴于点N.若点P在点Q左边,当矩形PQMN的周长最大时,求△AEM的面积;
(3)在(2)的条件下,当矩形PMNQ的周长最大时,连接DQ.过抛物线上一点F作y轴的平行线,与直线AC交于点G(点G在点F的上方).若FG=![]() DQ,求点F的坐标.
DQ,求点F的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着“三农”问题的解决,某农民近两年的年收入发生了明显变化,已知前年和去年的收入分别是60000元和80000元,下面是依据①②③三种农作物每种作物每年的收入占该年年收入的比例绘制的扇形统计图.依据统计图得出的以下四个结论正确的是( )
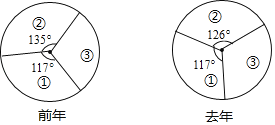
A. ①的收入去年和前年相同
B. ③的收入所占比例前年的比去年的大
C. 去年②的收入为2.8万
D. 前年年收入不止①②③三种农作物的收入
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=ax+b与x轴、y轴交于A、B两点,与反比例函数y=![]() 相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )
相交于C、D两点,分别过C、D两点作y轴、x轴的垂线,垂足为E、F,连接CF、DE、EF. 有下列三个结论:①△CEF与△DEF的面积相等;②△DCE≌△CDF;③AC=BD.其中正确的结论个数是( )
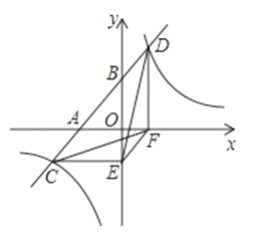
A. 0 B. 1 C. 2 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形ABCD绕点A顺时针旋转,使点B的对应点B落在DA的延长线上,若AB=2,BC=4,则点C与其对应点C的距离为( )
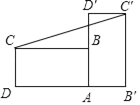
A. 6 B. 8 C. 2![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y﹣x称为P点的“坐标差”,记作Zp,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.
(1)①点A(3,1)的“坐标差”为_______;
②抛物线y=﹣x2+5x的“特征值”为________;
(2)某二次函数y=﹣x2+bx+c(c≠0)的“特征值”为﹣1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等.
①直接写出m=______;(用含c的式子表示)
②求此二次函数的表达式.
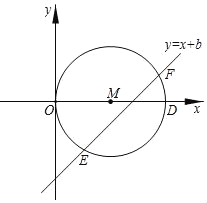
(3)如图,在平面直角坐标系xOy中,点D(4,0),以OD为直径作⊙M,直线y=x+b与⊙M相交于点E、F.
①比较点E、F的“坐标差”ZE、ZF的大小.
②请直接写出⊙M的“特征值”为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
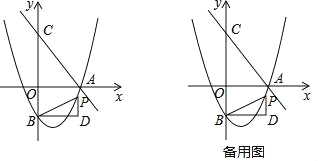
【题目】如图,直线y=﹣![]() x+n交x轴于点A,交y轴于点C(0,4),抛物线y=
x+n交x轴于点A,交y轴于点C(0,4),抛物线y=![]() x2+bx+c经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m.
x2+bx+c经过点A,交y轴于点B(0,﹣2).点P为抛物线上一个动点,过点P作x轴的垂线PD,过点B作BD⊥PD于点D,连接PB,设点P的横坐标为m.
(1)求抛物线的解析式;
(2)当△BDP为等腰直角三角形时,求线段PD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
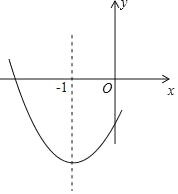
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象的对称轴为直线x=﹣1,下列结论正确的有_____(填序号).
①若图象过点(﹣3,y1)、(2,y2),则y1<y2;
②ac<0;
③2a﹣b=0;
④b2﹣4ac<0.
查看答案和解析>>
科目:初中数学 来源: 题型:
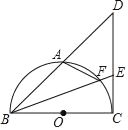
【题目】如图,BC为⊙O的直径,点A是弧BC的中点,连接BA并延长至点D,使得AD=AB,连接CD,点E为CD上一点,连接BE交弧BC于点F,连接AF.
(1)求证:CD为⊙O的切线;
(2)求证:∠DAF=∠BEC;
(3)若DE=2CE=4,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com