
【题目】定义:在平面直角坐标系中,图形G上点P(x,y)的纵坐标y与其横坐标x的差y﹣x称为P点的“坐标差”,记作Zp,而图形G上所有点的“坐标差”中的最大值称为图形G的“特征值”.
(1)①点A(3,1)的“坐标差”为_______;
②抛物线y=﹣x2+5x的“特征值”为________;
(2)某二次函数y=﹣x2+bx+c(c≠0)的“特征值”为﹣1,点B(m,0)与点C分别是此二次函数的图象与x轴和y轴的交点,且点B与点C的“坐标差”相等.
①直接写出m=______;(用含c的式子表示)
②求此二次函数的表达式.
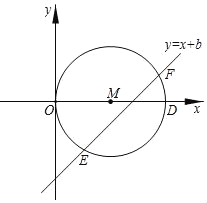
(3)如图,在平面直角坐标系xOy中,点D(4,0),以OD为直径作⊙M,直线y=x+b与⊙M相交于点E、F.
①比较点E、F的“坐标差”ZE、ZF的大小.
②请直接写出⊙M的“特征值”为_______.
【答案】(1)①-2;②4;(2)①-c;②y=﹣x2+3x﹣2;(3)①ZE=ZF;②2![]() ﹣2.
﹣2.
【解析】
(1)①由“坐标差”的定义可求出点A(3,1)的“坐标差”;
②用y﹣x可找出y﹣x关于x的函数关系式,再利用配方法即可求出y﹣x的最大值,进而可得出抛物线y=﹣x2+5x的“特征值”;
(2)①利用二次函数图象上点的坐标特征可求出点C的坐标,由“坐标差”的定义结合点B与点C的“坐标差”相等,即可求出m的值;
②由点B的坐标利用待定系数法可找出b,c之间的关系,找出y﹣x关于x的函数关系式,再利用二次函数的性质结合二次函数y=﹣x2+bx+c(c≠0)的“特征值”为﹣1,即可得出关于b的一元二次方程,解之即可得出b的值,进而可得出c的值,此问得解;
(3)①利用一次函数图象上点的坐标特征可设点E的坐标为(xE,xE+b),点F的坐标为(xF,xF+b),结合“坐标差”的定义可得出ZE=ZF;
②作直线y=x+n(n>0)与⊙M相切,设切点为N,该直线与x轴交于点Q,利用等腰直角三角形的性质可求出点Q的坐标,再利用待定系数法可求出n值,结合“特征值”的定义即可找出⊙M的“特征值”.
(1)①1﹣3=﹣2.
故答案为:﹣2.
②y﹣x=﹣x2+5x﹣x=﹣(x﹣2)2+4,
∵﹣1<0,
∴当x=2时,y﹣x取得最大值,最大值为4.
故答案为:4.
(2)①当x=0时,y=﹣x2+bx+c=c,
∴点C的坐标为(0,c).
∵点B与点C的“坐标差”相等,
∴0﹣m=c﹣0,
∴m=﹣c.
故答案为:﹣c.
②由①可知:点B的坐标为(﹣c,0).
将点B(﹣c,0)代入y=﹣x2+bx+c,得:0=﹣c2﹣bc+c,
∴c1=1﹣b,c2=0(舍去).
∵二次函数y=﹣x2+bx+c(c≠0)的“特征值”为﹣1,
∴y﹣x=﹣x2+(b﹣1)x+1﹣b的最大值为﹣1,
∴![]() =-1,
=-1,
解得:b=3,
∴c=1﹣b=﹣2,
∴二次函数的解析式为y=﹣x2+3x﹣2.
(3)①∵点E,F在直线y=x+b上,
∴设点E的坐标为(xE,xE+b),点F的坐标为(xF,xF+b),
∴ZE=xE+b﹣xE=b,ZF=xF+b﹣xF=b,
∴ZE=ZF.
②作直线y=x+n(n>0)与⊙M相切,设切点为N,该直线与x轴交于点Q,如图所示.

∵y﹣x=x+n﹣x=n,
∴当直线y=x+n(n>0)与⊙M相切时,y﹣x的值为⊙M的“特征值”.
∵∠NQM=45°,MN⊥NQ,MN=2,
∴△MNQ为等腰直角三角形,
∴MQ=2![]() ,
,
∴点Q的坐标为(2﹣2![]() ,0).
,0).
将Q(2﹣2![]() ,0)代入y=x+n,得:0=2﹣2
,0)代入y=x+n,得:0=2﹣2![]() +n,
+n,
解得:n=2![]() ﹣2,
﹣2,
∴⊙M的“特征值”为2![]() ﹣2.
﹣2.
故答案为:2![]() ﹣2.
﹣2.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
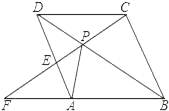
【题目】如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
(1)图中△APD与哪个三角形全等:_____.
(2)猜想:线段PC、PE、PF之间存在什么关系:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展了为期一周的“敬老爱亲”社会活动,为了解情况,学生会随机调查了部分学生在这次活动中做家务的时间,并将统计的时间(单位:小时)分成5组,A:0.5≤x<1,B:1≤x<1.5,C:1.5≤x<2,D:2≤x<2.5,E:2.5≤x<3,制作成两幅不完整的统计图(如图).
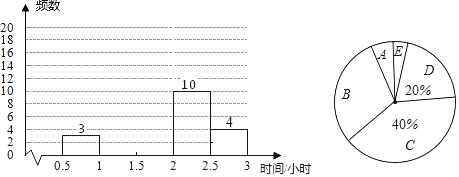
请根据图中提供的信息,解答下列问题:
(1)学生会随机调查了 名学生;
(2)补全频数分布直方图;
(3)若全校有1800名学生,估计该校在这次活动中做家务的时间不少于2.5小时的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,正比例函数![]() 与反比例函数
与反比例函数![]() 的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为
的图象分别交于A、C两点,已知点B与点D关于坐标原点O成中心对称,且点B的坐标为![]() 其中
其中![]() .
.
![]() 四边形ABCD的是______
四边形ABCD的是______![]() 填写四边形ABCD的形状
填写四边形ABCD的形状![]()
![]() 当点A的坐标为
当点A的坐标为![]() 时,四边形ABCD是矩形,求m,n的值.
时,四边形ABCD是矩形,求m,n的值.
![]() 试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.
试探究:随着k与m的变化,四边形ABCD能不能成为菱形?若能,请直接写出k的值;若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为16cm的等腰直角三角形.
(1)在等腰直角三角形ABC纸片中,以C为圆心,剪出一个面积最大的扇形(要求:尺规作图,保留作图痕迹,不写作法);
(2)请求出所制作圆锥底面的半径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△AOB中,∠O=90°,AO=18cm,BO=30cm,动点M从点A开始沿边AO以1cm/s的速度向终点O移动,动点N从点O开始沿边OB以2cm/s的速度向终点B移动,一个点到达终点时,另一个点也停止运动.如果M、N两点分别从A、O两点同时出发,设运动时间为ts时四边形ABNM的面积为Scm2.
(1)求S关于t的函数关系式,并直接写出t的取值范围;
(2)判断S有最大值还是有最小值,用配方法求出这个值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C是AB延长线上一点,CD与⊙O相切于点E,AD⊥CD于点D.
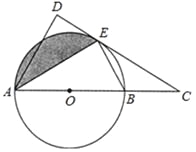
(1)求证:AE平分∠DAC;
(2)若AB=4,∠ABE=60°.
①求AD的长;
②求出图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量某建筑物EF的高度,小明在楼AB上选择观测点A、C,从A测得建筑物的顶部E的仰角为37°,从C测得建筑物的顶部E的仰角为45°,A处高度为20m,C处高度为10m.求建筑物EF的高度(精确到1m).
(参考数据:sin37°≈0.6,cos37°≈0.8,tan37≈0.75,![]() ≈1.4)
≈1.4)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com