
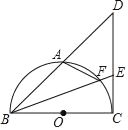
【题目】如图,BC为⊙O的直径,点A是弧BC的中点,连接BA并延长至点D,使得AD=AB,连接CD,点E为CD上一点,连接BE交弧BC于点F,连接AF.
(1)求证:CD为⊙O的切线;
(2)求证:∠DAF=∠BEC;
(3)若DE=2CE=4,求AF的长.
【答案】(1)见解析;(2)见解析;(3)AF=![]() .
.
【解析】
(1)欲证明CD是⊙O的切线,只要证明DC⊥BC即可;
(2)利用等角的余角相等证明即可;
(3)由△ABF∽△EBD,可得AF:DE=AB:BE,只要求出AB,BE即可解决问题;
(1)证明:连接AC.
∵![]() ,
,
∴AB=AC,
∵AB=AD,
∴AC=AB=AD,
∴∠BCD=90°,
∴CD⊥BC,
∴CD是⊙O的切线.
(2)解:∵BC是直径,
∴∠BAC=∠CAD=90°,
∴∠DAF+∠CAF=90°,
∵∠BCE=90°
∴∠BEC+∠CBE=90°,
∵∠CBE=∠CAF,
∴∠DAF=∠BEC.
(3)解:∵AB=BD,CA⊥BD,
∴CD=BC,
∴△BCD是等腰直角三角形,
∴∠ACB=∠AFB=∠D=45°,
∵∠ABF=∠DBE,
∴△ABF∽△EBD,
∴AF:DE=AB:BE,
∵DE=2EC=4,
∴BC=CD=6,AB=3![]() ,BE=
,BE=![]() ,
,
∴AF=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在数学活动课中,同学们准备了一些等腰直角三角形纸片,从每张纸片中剪出一个扇形制作圆锥玩具模型.如图,已知△ABC是腰长为16cm的等腰直角三角形.
(1)在等腰直角三角形ABC纸片中,以C为圆心,剪出一个面积最大的扇形(要求:尺规作图,保留作图痕迹,不写作法);
(2)请求出所制作圆锥底面的半径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
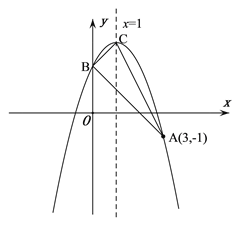
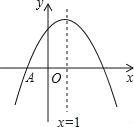
【题目】如图,抛物线![]() 的顶点为C,对称轴为直线
的顶点为C,对称轴为直线![]() ,且经过点A(3,-1),与y轴交于点B.
,且经过点A(3,-1),与y轴交于点B.
(1)求抛物线的解析式;
(2)判断△ABC的形状,并说明理由;
(3)经过点A的直线交抛物线于点P,交x轴于点Q,若![]() ,试求出点P的坐标.
,试求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),顶点坐标(1,n),与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②﹣1≤a≤﹣![]() ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一辆客车从甲地出发前往乙地,平均速度v(千米/小时)与所用时间t(小时)的函数关系如图所示,其中60≤v≤120.
(1)直接写出v与t的函数关系式;
(2)若一辆货车同时从乙地出发前往甲地,客车比货车平均每小时多行驶20千米,3小时后两车相遇.
①求两车的平均速度;
②甲、乙两地间有两个加油站A、B,它们相距200千米,当客车进入B加油站时,货车恰好进入A加油站(两车加油的时间忽略不计),求甲地与B加油站的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
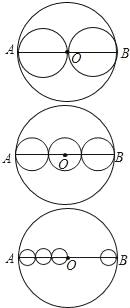
【题目】如图,AB是⊙O的直径,把AB分成几条相等的线段,以每条线段为直径分别画小圆,设AB=a,那么⊙O的周长l=πa.
计算:(1)把AB分成两条相等的线段,每个小圆的周长![]() ;
;
(2)把AB分成三条相等的线段,每个小圆的周长l3= ;
(3)把AB分成四条相等的线段,每个小圆的周长l4= ;
(4)把AB分成n条相等的线段,每个小圆的周长ln= .
结论:把大圆的直径分成n条相等的线段,以每条线段为直径分别画小圆,那么每个小圆周长是大圆周长的 .请仿照上面的探索方法和步骤,计算推导出每个小圆面积与大圆面积的关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.

(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com