
【题目】某坦克部队需要经过一个拱桥(如图所示),拱桥的轮廓是抛物线形,拱高OC=6m,跨度AB=20m,有5根支柱:AG、MN、CD、EF、BH,相邻两支柱的距离均为5m.
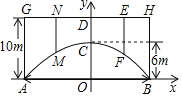
(1)以AB的中点为原点,AB所在直线为x轴,支柱CD所在直线为y轴,建立平面直角坐标系,求抛物线的解析式;
(2)若支柱每米造价为2万元,求5根支柱的总造价;
(3)拱桥下面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道是坦克的行进方向,现每辆坦克长4m,宽2m,高3m,行驶速度为24km/h,坦克允许并排行驶,坦克前后左右距离忽略不计,试问120辆该型号坦克从刚开始进入到全部通过这座长1000m的拱桥隧道所需最短时间为多少分钟?
【答案】(1)y=﹣![]() x2+6;(2)70万元;(3)2.9分
x2+6;(2)70万元;(3)2.9分
【解析】
(1)根据题目可知A,B,C的坐标,设出抛物线的解析式代入可求解.
(2)把x=5代入可求出支柱的长度,然后算出总造价即可.
(3)先求出坦克方队的长,然后算出速度,从而求得通过隧道的时间即可.
(1)设y=ax2+c,把C(0,6)、B(10,0)代入,
得![]() .
.
∴y=﹣![]() x2+6.
x2+6.
(2)当x=5时,y=﹣![]() ×52+6=
×52+6=![]() ,
,
∴EF=10﹣![]() =
=![]() ,CD=10﹣6=4,
,CD=10﹣6=4,
支柱的总造价为2(2×![]() +2×10+4)=70(万元).
+2×10+4)=70(万元).
(3)∵坦克的高为3米,令y=3时,﹣![]() x2+6=3,
x2+6=3,
解得:x=±5![]() ,
,
∵7<5![]() <8,坦克宽为2米,
<8,坦克宽为2米,
∴可以并排3辆坦克行驶,此时坦克方阵的长为120÷3×4=160(米),
坦克的行驶速度为24km/h=400米/分,
∴通过隧道的最短时间为![]() =2.9(分).
=2.9(分).


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:初中数学 来源: 题型:
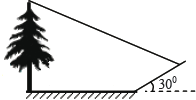
【题目】小明想测量一棵树的高度,他发现树的影子恰好落在地面和一斜坡上;如图,此时测得地面上的影长为8米,坡面上的影长为4米.已知斜坡的坡角为300,同一时 刻,一根长为l米、垂直于地面放置的标杆在地面上的影长为2米,则树的高度为【 】
A.![]() 米 B.12米 C.
米 B.12米 C.![]() 米 D.10米
米 D.10米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点A与⊙O上所有点的连线段中,长度的最小值称为点A到⊙O的最小距离,记为mA;点A与⊙O上所有点的连线段中,长度的最大值称为点A到⊙O的最大距离,记为MA,如图,⊙O的半径为r,点A在⊙O外,且OA=d,则mA=d﹣r.证明如下:
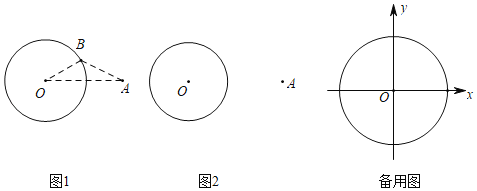
证明:如图1,设B为圆上任意一点,连结OA、OB、AB
①当O、A、B不共线时,AB>OA﹣OB
即AB>d﹣r
②当O、A、B共线时,AB=OA﹣OB
即AB=d﹣r
综上,AB≥d﹣r,即mA=d﹣r
(1)利用刚才的证明,结合所给的图2,⊙O的半径为r,点A在⊙O外,且OA=d,探究MA,你的结论是MA= ,请证明你的结论;
(2)已知⊙O的半径为2,mA=4,则MA= ;
(3)在平面直角坐标系中,以原点O为圆心,6为半径作⊙O,第二象限的点A的坐标为(﹣3,a),且mA=1,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
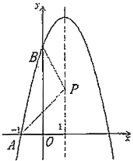
【题目】已知抛物线![]() 在坐标系中的位置如图所示,它与
在坐标系中的位置如图所示,它与![]() ,
,![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,
,![]() 是其对称轴
是其对称轴![]() 上的动点,根据图中提供的信息,给出以下结论:①
上的动点,根据图中提供的信息,给出以下结论:①![]() ,②
,②![]() 是
是![]() 的一个根,③若
的一个根,③若![]() ,
,![]() ,则
,则![]() .其中正确的有______个.
.其中正确的有______个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() ,
,![]() 两点,交
两点,交![]() 轴于点
轴于点![]() .直线
.直线![]() 经过点
经过点![]() ,
,![]() .
.
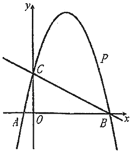
(1)求抛物线的解析式;
(2)点![]() 是直线
是直线![]() 上方抛物线上一动点,设点
上方抛物线上一动点,设点![]() 的横坐标为
的横坐标为![]() .
.
①求![]() 面积最大值和此时
面积最大值和此时![]() 的值;
的值;
②![]() 是直线
是直线![]() 上一动点,是否存在点
上一动点,是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,若存在,直接写出点
为顶点的四边形是平行四边形,若存在,直接写出点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,C分别在x轴,y轴上,四边形ABCO为矩形,AB=16,点D与点A关于y轴对称,tan∠ACB=![]() ,点E、F分别是线段AD、AC上的动点,(点E不与点A,D重合),且∠CEF=∠ACB.
,点E、F分别是线段AD、AC上的动点,(点E不与点A,D重合),且∠CEF=∠ACB.
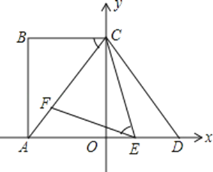
(1)求AC的长和点D的坐标;
(2)求证:![]() ;
;
(3)当△EFC为等腰三角形时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着中央电视台《朗读者》节目的播出,“朗读”为越来越多的同学所喜爱,西宁市某中学计划在全校开展“朗读”活动,为了了解同学们对这项活动的参与态度,随机对部分学生进行了一次调查,调查结果整理后,将这部分同学的态度划分为四个类别:![]() .积极参与,
.积极参与,![]() .一定参与,
.一定参与,![]() .可以参与,
.可以参与,![]() .不参与.根据调查结果制作了如下不完整的统计表和统计图.
.不参与.根据调查结果制作了如下不完整的统计表和统计图.
学生参与“朗读”的态度统计表
类别 | 人数 | 所占百分比 |
| 18 |
|
| 20 |
|
|
|
|
| 4 |
|
合计 |
|
|
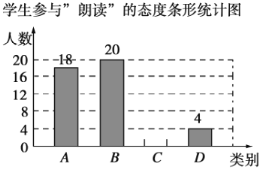
请你根据以上信息,解答下列问题:
(1)![]() ______,
______,![]() ______,并将条形统计图补充完整;
______,并将条形统计图补充完整;
(2)该校有1500名学生,如果“不参与”的人数不超过150人时,“朗读”活动可以顺利开展,通过计算分析这次活动能否顺利开展?
(3)“朗读”活动中,九年级一班比较优秀的四名同学恰好是两男两女,从中随机选取两人在班级进行朗读示范,试用画树状图法或列表法求所选两人都是女生的概率,并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
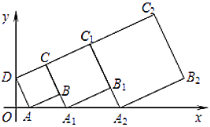
【题目】在平面坐标系中,正方形![]() 的位置如图所示,点
的位置如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ,正方形
,正方形![]() 的面积为______,延长
的面积为______,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ,……按这样的规律进行下去,正方形
,……按这样的规律进行下去,正方形![]() 的面积为______.
的面积为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com