
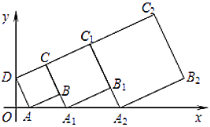
【题目】在平面坐标系中,正方形![]() 的位置如图所示,点
的位置如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ,正方形
,正方形![]() 的面积为______,延长
的面积为______,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ,……按这样的规律进行下去,正方形
,……按这样的规律进行下去,正方形![]() 的面积为______.
的面积为______.
【答案】11.25 
【解析】
推出AD=AB,∠DAB=∠ABC=∠ABA1=90°=∠DOA,求出∠ADO=∠BAA1,证△DOA∽△ABA1,再求出AB,BA1,面积即可求出;求出第2个正方形的边长;再求出第3个正方形边长;依此类推得出第2019个正方形的边长,求出面积即可.
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠ABC=∠ABA1=90°=∠DOA,
∴∠ADO+∠DAO=90°,∠DAO+∠BAA1=90°,
∴∠ADO=∠BAA1,
∵∠DOA=∠ABA1,
∴△DOA∽△ABA1,
∴![]() ,
,
∵AB=AD=![]() ,
,
∴BA1=![]() ,
,
∴第2个正方形A1B1C1C的边长A1C=A1B+BC=![]() ,
,
第2个正方形A1B1C1C的面积(![]() )2=11.25
)2=11.25
同理第3个正方形的边长是=(![]() )2
)2![]() ,
,
第4个正方形的边长是(![]() )3
)3![]() ,,
,,
第2019个正方形的边长是(![]() )2018
)2018![]() ,
,
面积是[(![]() )2018
)2018![]() ]2=5×(
]2=5×(![]() )2018×2=
)2018×2=![]()
故答案为:(1)11.25;(2)![]()


科目:初中数学 来源: 题型:
【题目】某坦克部队需要经过一个拱桥(如图所示),拱桥的轮廓是抛物线形,拱高OC=6m,跨度AB=20m,有5根支柱:AG、MN、CD、EF、BH,相邻两支柱的距离均为5m.
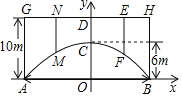
(1)以AB的中点为原点,AB所在直线为x轴,支柱CD所在直线为y轴,建立平面直角坐标系,求抛物线的解析式;
(2)若支柱每米造价为2万元,求5根支柱的总造价;
(3)拱桥下面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道是坦克的行进方向,现每辆坦克长4m,宽2m,高3m,行驶速度为24km/h,坦克允许并排行驶,坦克前后左右距离忽略不计,试问120辆该型号坦克从刚开始进入到全部通过这座长1000m的拱桥隧道所需最短时间为多少分钟?
查看答案和解析>>
科目:初中数学 来源: 题型:
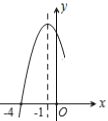
【题目】二次函数![]() 的部分图象如图所示,图象过点
的部分图象如图所示,图象过点![]() ,对称轴为直线
,对称轴为直线![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③一元二次方程
;③一元二次方程![]() 的解是
的解是![]() ,
,![]() ;④当
;④当![]() 时,
时,![]() ,其中正确的结论有__________.
,其中正确的结论有__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
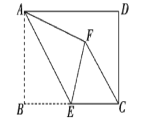
【题目】如图,在矩形ABCD中,AB=4,BC=6,点E为BC的中点,将△ABE沿AE折叠,使点B落在矩形内点F处,连接CF,则CF的长度为_____
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的布袋里装有![]() 个标号分别为
个标号分别为![]() 的小球,这些球除标号外无其它差别.从布袋里随机取出一个小球,记下标号为
的小球,这些球除标号外无其它差别.从布袋里随机取出一个小球,记下标号为![]() ,再从剩下的
,再从剩下的![]() 个小球中随机取出一个小球,记下标号为
个小球中随机取出一个小球,记下标号为![]() 记点
记点![]() 的坐标为
的坐标为![]() .
.
(1)请用画树形图或列表的方法写出点![]() 所有可能的坐标;
所有可能的坐标;
(2)求两次取出的小球标号之和大于![]() 的概率;
的概率;
(3)求点![]() 落在直线
落在直线![]() 上的概率.
上的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com