练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图是水平放置的水管截面示意图，已知水管的半径为50cm，水面宽AB=80cm，则水深CD约为______cm．

    【答案】20

    【解析】

    连接OA，设CD为x，由于C点为弧AB的中点，CD⊥AB，根据垂径定理的推理和垂径定理得到CD必过圆心0，即点O、D、C共线，AD=BD=AB=40，在Rt△OAD中，利用勾股定理得（50-x）2+402=502，然后解方程即可．

    解：连接OA、如图，设⊙O的半径为R，


    ∵CD为水深，即C点为弧AB的中点，CD⊥AB，

    ∴CD必过圆心O，即点O、D、C共线，AD=BD=AB=40，
    在Rt△OAD中，OA=50，OD=50-x，AD=40，
    ∵OD2+AD2=OA2，
    ∴（50-x）2+402=502，解得x=20，
    即水深CD约为为20．
    故答案为；20

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】以下是某市自来水价格调整表(部分)：(单位：元/立方米)

    用水类别

    现行水价

    拟调整水价

    一、居民生活用水

    0.72

    1、一户一表

    第一阶梯：月用水量0～30立方米/户

    0.82

    第二阶梯：月用水量超过30立方米/户部分

    1.23

    则调整水价后某户居民月用水量x(立方米)与应交水费y(元)的函数图象是(　　)

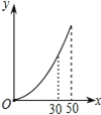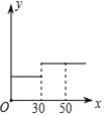    A.B.C.D.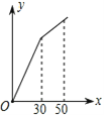

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】居民区内的“广场舞”引起媒体关注，辽宁都市频道为此进行过专访报道．小平想了解本小区居民对“广场舞”的看法，进行了一次抽样调查，把居民对“广场舞”的看法分为四个层次：A．非常赞同；B．赞同但要有时间限制；C．无所谓；D．不赞同．并将调查结果绘制了图1和图2两幅不完整的统计图．

    请你根据图中提供的信息解答下列问题：

    （1）求本次被抽查的居民有多少人？

    （2）将图1和图2补充完整；

    （3）求图2中“C”层次所在扇形的圆心角的度数；

    （4）估计该小区4000名居民中对“广场舞”的看法表示赞同（包括A层次和B层次）的大约有多少人．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，矩形A1B1C1D1的面积为4，顺次连结各边中点得到四边形A2B2C2D2，再顺次连结四边形A2B2C2D2四边中点得到四边形A3B3C3D3，依此类推，则四边形AnBnCnDn的面积是　 　．

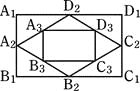
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知与均是等边三角形，点在同一条直线上，与交于点，与交于点，与交于点，连接，则下列结论：①；②；③；④，其中正确的个数是（ ）

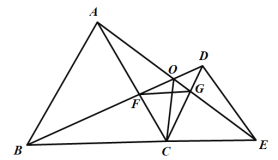
    A.1B.2C.3D.4

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店将每件进价为80元的某种商店按每件110元出售，每天可售出100件．该商店想通过降低售价、增加销售量的方法来提高利润．经市场调查，发现这种商品每件每降价5元，每天的销售量可增加50件．设商品降价x元，每天销售该商品获得的利润为y元．

    （1）求y（元）关于x（元）的函数关系式，并写出x的取值范围．

    （2）求当x取何值时y最大？并求出y的最大值．

    （3）若要是每天销售利润为3750元，且尽可能最大的向顾客让利，应将该商品降价多少元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AB=AC，D为BC边上一点，∠B=30°∠DAB=45°．（1）求∠DAC的度数；（2）请说明：AB=CD．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，甲、乙两人以相同路线前往距离单位10km的培训中心参加学习，图中1， 分别表示甲、乙两人前往目的地所走的路程S(千米)随时间(分)变化的函数图象，以下说法:①甲比乙提前12分钟到达；②甲的平均速度为15千米/小时；③甲、乙相遇时，乙走了6千米；④乙出发6分钟后追上甲，其中正确的是( )

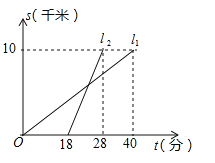
    A.①②B.③④C.①③④D.②③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，矩形的一条边长为x，周长的一半为y，定义（x，y）为这个矩形的坐标。如图2，在平面直角坐标系中，直线x=1，y=3将第一象限划分成4个区域，已知矩形1的坐标的对应点A落在如图所示的双曲线上，矩形2的坐标的对应点落在区域④中，则下面叙述中正确的是（ ）

    A. 点A的横坐标有可能大于3

    B. 矩形1是正方形时，点A位于区域②

    C. 当点A沿双曲线向上移动时，矩形1的面积减小

    D. 当点A位于区域①时，矩形1可能和矩形2全等

    查看答案和解析>>

    同步练习册答案