
【题目】如图,在边长为![]() 的正方形
的正方形![]() 中,点
中,点![]() ,
,![]() ,
,![]() ,
,![]() 分别按
分别按![]() ,
,![]() ,
,![]() ,
,![]() 的方向同时出
的方向同时出

发,以![]() 的速度匀速运动.在运动过程中,设四边形
的速度匀速运动.在运动过程中,设四边形![]() 的面积为
的面积为![]() ,运动时间为
,运动时间为![]() .
.
![]() 试证明四边形
试证明四边形![]() 是正方形;
是正方形;
![]() 写出
写出![]() 关于
关于![]() 的函数关系式,并求运动几秒钟时,面积最小,最小值是多少?
的函数关系式,并求运动几秒钟时,面积最小,最小值是多少?
![]() 是否存在某一时刻
是否存在某一时刻![]() ,使四边形
,使四边形![]() 的面积与正方形
的面积与正方形![]() 的面积比是
的面积比是![]() ?若存在,求出
?若存在,求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】![]() 证明见解析;
证明见解析;![]() 秒时,
秒时,![]() 有最小值,最小值是
有最小值,最小值是![]() ;
;![]() 或
或![]() 时,四边形
时,四边形![]() 的面积与正方形
的面积与正方形![]() 的面积的比是
的面积的比是![]() .
.
【解析】
根据四个点的速度相同可知![]() ,根据正方形的性质可证明
,根据正方形的性质可证明![]() 可证明四边形
可证明四边形![]() 是菱形,根据
是菱形,根据![]() ,
,![]() ,可知
,可知![]() ,即可证明四边形
,即可证明四边形![]() 为正方形. (2)时间为t
为正方形. (2)时间为t![]() ,速度为1
,速度为1![]() ,则AE=t,AH=4-t,即可知S关于t的关系式.根据关系式即可求出最小值与最大值.(3)根据边长可求出正方形ABCD的面积,再根据面积比,结合(2)所求关系式即可求出t的值.
,则AE=t,AH=4-t,即可知S关于t的关系式.根据关系式即可求出最小值与最大值.(3)根据边长可求出正方形ABCD的面积,再根据面积比,结合(2)所求关系式即可求出t的值.
![]() ∵点
∵点![]() ,
,![]() ,
,![]() ,
,![]() 在四条边上的运动速度相同,
在四条边上的运动速度相同,
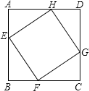
∴![]() ,
,
在正方形![]() 中,
中,![]() ,
,
且![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() (全等三角形的对应边相等),
(全等三角形的对应边相等),
![]() (全等三角形的对应角相等),
(全等三角形的对应角相等),
∴四边形![]() 是菱形.(四条边相等的四边形是菱形),
是菱形.(四条边相等的四边形是菱形),
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴四边形![]() 为正方形.(有一个角是直角的菱形是正方形).
为正方形.(有一个角是直角的菱形是正方形).
![]() ∵运动时间为
∵运动时间为![]() ,运动速度为
,运动速度为![]() ,
,
∴![]() ,
,![]() ,
,
由![]() 知四边形
知四边形![]() 为正方形,
为正方形,
∴![]()
即![]() ,
,
当![]() 秒时,
秒时,![]() 有最小值,最小值是
有最小值,最小值是![]() ;
;
![]() 存在某一时刻
存在某一时刻![]() ,使四边形
,使四边形![]() 的面积与正方形
的面积与正方形![]() 的面积比是
的面积比是![]() .
.
∵![]() ,
,
∴![]() ,∴
,∴![]() ,
,![]() ;
;
当![]() 或
或![]() 时,
时,
四边形![]() 的面积与正方形
的面积与正方形![]() 的面积的比是
的面积的比是![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】阅读下面的文字后,解答问题:
有这样一道题目:“如图,E、D是△ABC中BC边上的两点,AD=AE, .求证△ABE≌△ACD.请根据你的理解,在题目中的空格内,把原题补充完整(添加一个适当的条件),并写出证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠A=36°,AC的垂直平分线交AB于E,D为垂足,连接EC,若CE=5,则BC等于( )
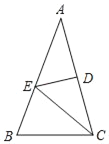
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图![]() ,分别沿长方形纸片
,分别沿长方形纸片![]() 和正方形纸片
和正方形纸片![]() 的对角线
的对角线![]() ,
,![]() 剪开,拼成如图
剪开,拼成如图![]() 所示的四边形
所示的四边形![]() ,若中间空白部分四边形恰好是正方形
,若中间空白部分四边形恰好是正方形![]() ,且四边形
,且四边形![]() 的面积为
的面积为![]() ,则正方形的面积是( )
,则正方形的面积是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读解答:
分解下列因式:![]() ,
,![]() ,
,![]()
(1)观察上述三个多项式的系数,有![]() ,
,![]() ,
,![]() ,
,
于是某同学猜测:若多项式![]() 是完全平方式,那么实系数
是完全平方式,那么实系数![]() ,
,![]() ,
,![]() 之间一定存在某种关系,请你用数学式子表示系数
之间一定存在某种关系,请你用数学式子表示系数![]() ,
,![]() ,
,![]() 之间的关系_______.
之间的关系_______.
(2)解决问题:在实数范围内,若关于 x 的多项式![]() 是完全平方式,且
是完全平方式,且![]() 、
、![]() 都是正整数,
都是正整数,![]() ,求
,求![]() 、
、![]() 的值;
的值;
(3)在实数范围内,若关于![]() 的多项式
的多项式![]() 和
和![]() 都是完全平方式,利用(1)中的规律,求
都是完全平方式,利用(1)中的规律,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A、F、E、C在同一直线上,AB∥CD,∠ABE=∠CDF,AF=CE.
(1)从图中任找两组全等三角形;
(2)从(1)中任选一组进行证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形OABC的顶点O是原点,顶点B在y轴上,两条对角线AC、OB的长分别是6和4,反比例函数![]() 的图象经过点C.
的图象经过点C.
(1)写出点A的坐标,并求k的值;
(2)将菱形OABC沿y轴向下平移多少个单位长度后点A会落在该反比例函数的图象上?
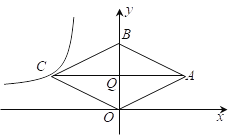
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高节水意识,小申随机统计了自己家7天的用水量,并分析了第3天的用水情况,将得到的数据进行整理后,绘制成如图所示的统计图.(单位:升)
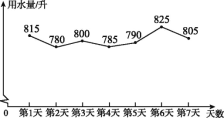
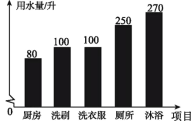
(1)求这7天内小申家每天用水量的平均数和中位数;
(2)求第3天小申家洗衣服的水占这一天总用水量的百分比;
(3)请你根据统计图中的信息,给小申家提出一条全理的节约用水建议,并估算采用你的建议后小申家一个月(按30天计算)的节约用水量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com