
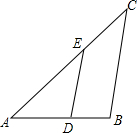
 如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=7cm,∠BAC=45°,∠C=40°.
如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=7cm,∠BAC=45°,∠C=40°.分析 (1)由三角形内角和定理求出∠B=95°,由相似三角形的性质得出∠AED=∠C=40°,∠ADE=∠B=95°即可;
(2)由相似三角形的对应边成比例得出$\frac{AE}{AC}=\frac{DE}{BC}$,即可得出DE的长.
解答 解:(1)∵∠BAC=45°,∠C=40°,
∴∠B=180°-45°-40°=95°,
∵△ABC∽△ADE,
∴∠AED=∠C=40°,∠ADE=∠B=95°;
(2)∵△ABC∽△ADE,
∴$\frac{AE}{AC}=\frac{DE}{BC}$,
即$\frac{5}{5+3}=\frac{DE}{7}$,
解得:DE=$\frac{35}{8}$(cm).
点评 本题考查了相似三角形的性质、三角形内角和定理;熟练掌握相似三角形的性质是解决问题的关键.


科目:初中数学 来源: 题型:填空题
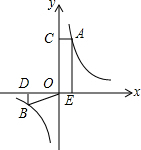 如图所示,点A、B分别是反比例函数图象上的点,AE⊥x轴于点E,AC⊥y轴于点C,BD⊥x轴于点D,连接BO,若四边形ACOE的面积为12cm2,则△OBD的面积为6cm2.
如图所示,点A、B分别是反比例函数图象上的点,AE⊥x轴于点E,AC⊥y轴于点C,BD⊥x轴于点D,连接BO,若四边形ACOE的面积为12cm2,则△OBD的面积为6cm2.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
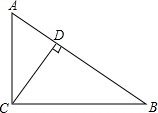 如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,tan∠ACD=$\frac{3}{4}$,AB=5,那么CD的长是$\frac{12}{5}$.
如图,在Rt△ABC中,∠ACB=90°,CD⊥AB,垂足为D,tan∠ACD=$\frac{3}{4}$,AB=5,那么CD的长是$\frac{12}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
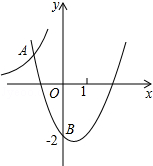 如图,二次函数y=x2+bx+c的图象过点B(0,-2).它与反比例函数y=-$\frac{12}{x}$的图象交于点A(m,4),求这个二次函数的解析式.
如图,二次函数y=x2+bx+c的图象过点B(0,-2).它与反比例函数y=-$\frac{12}{x}$的图象交于点A(m,4),求这个二次函数的解析式.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
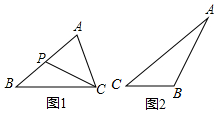 王华在学习相似三角形时,在北京市义务教育教科书九年级上册第31页遇到这样一道题,如图1,在△ABC中,P是边AB上的一点,连接CP,要使△ACP∽△ABC,还需要补充的一个条件是∠ACP=∠B(或∠APC=∠ACB),或AC2=AP•AB.
王华在学习相似三角形时,在北京市义务教育教科书九年级上册第31页遇到这样一道题,如图1,在△ABC中,P是边AB上的一点,连接CP,要使△ACP∽△ABC,还需要补充的一个条件是∠ACP=∠B(或∠APC=∠ACB),或AC2=AP•AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com