
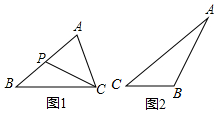
 王华在学习相似三角形时,在北京市义务教育教科书九年级上册第31页遇到这样一道题,如图1,在△ABC中,P是边AB上的一点,连接CP,要使△ACP∽△ABC,还需要补充的一个条件是∠ACP=∠B(或∠APC=∠ACB),或AC2=AP•AB.
王华在学习相似三角形时,在北京市义务教育教科书九年级上册第31页遇到这样一道题,如图1,在△ABC中,P是边AB上的一点,连接CP,要使△ACP∽△ABC,还需要补充的一个条件是∠ACP=∠B(或∠APC=∠ACB),或AC2=AP•AB.分析 (1)由∠A=∠A,当∠ACP=∠B,或∠APC=∠ACB;或$\frac{AC}{AB}=\frac{AP}{AC}$时,△ACP∽△ABC;
(2)延长AB到点D,使BD=BC,连接CD,由已知条件得出证出$\frac{AC}{AD}=\frac{AB}{AC}$,由∠A=∠A,证出△ACB∽△ADC,得出对应角相等∠ACB=∠D,再由等腰三角形的性质和三角形内角和定理得出∠ACB+∠BCD+∠D+∠A=180°,得出∠ACB=50°即可.
解答 解:∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB;
或$\frac{AC}{AB}=\frac{AP}{AC}$,即AC2=AP•AB时,△ACP∽△ABC;
故答案为:∠ACP=∠B(或∠APC=∠ACB),或AC2=AP•AB;
(1)王华补充的条件是:∠ACP=∠B(或∠APC=∠ACB);或AC2=AP•AB;理由如下:
∵∠A=∠A,
∴当∠ACP=∠B,或∠APC=∠ACB;
或$\frac{AC}{AB}=\frac{AP}{AC}$,即AC2=AP•AB时,△ACP∽△ABC;
故答案为:∠ACP=∠B(或∠APC=∠ACB),或AC2=AP•AB;
(2)延长AB到点D,使BD=BC,连接CD,如图所示:
∵AC2=AB2+AB•BC=AB(AB+BC)=AB(AB+BD)=AB•AD,
∴$\frac{AC}{AD}=\frac{AB}{AC}$,
又∵∠A=∠A,∴△ACB∽△ADC,
∴∠ACB=∠D,
∵BC=BD,
∴∠BCD=∠D,
在△ACD中,∠ACB+∠BCD+∠D+∠A=180°,
∴3∠ACB+30°=180°,
∴∠ACB=50°.
点评 本题考查了相似三角形的判定与性质、等腰三角形的性质、三角形内角和定理;本题中(2)有一定难度,需要通过作辅助线证明三角形相似才能得出结果.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
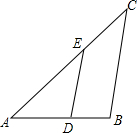 如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=7cm,∠BAC=45°,∠C=40°.
如图,已知△ABC∽△ADE,AE=5cm,EC=3cm,BC=7cm,∠BAC=45°,∠C=40°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的任意一点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的任意一点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com