
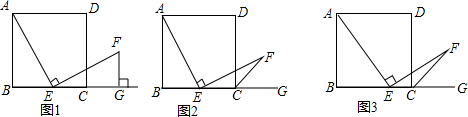
���� ��1�����ݡ�AEF=90�㣬���ɵõ���AEB+��FEG=90�㣬��ֱ�ǡ�ABE�У������������ڽǺͶ����õ���BAE+��AEB=90�㣬Ȼ�����ͬ�ǵ������ȣ�����֤�ã�
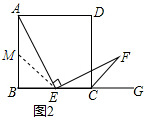
��2����AB���е�M������ME������ASA����֤����AME�ա�ECF��Ȼ�����ȫ�������εĶ�Ӧ����ȼ���֤�ã�
��3����AB��ȡһ��M��ʹAM=EC������ME��ͬ��2������ASA����֤����AME�ա�ECF��Ȼ�����ȫ�������εĶ�Ӧ����ȼ���֤�ã�
���  �⣺��1���ߡ�AEF=90�㣬
�⣺��1���ߡ�AEF=90�㣬
���AEB+��FEG=90�㣬
�֡�ֱ�ǡ�ABE�У���BAE+��AEB=90�㣬
���BAE=��FEG��
��2����AB���е�M������ME��
��������ABCD��AB=BC��
�֡�AM=MB=$\frac{1}{2}$AB��BE=CE=$\frac{1}{2}$BC��
��MB=BE��
���MBE�ǵ���ֱ�������Σ�
���BME=45�㣬
���AME=135�㣬
�֡ߡ�ECF=180��-��FCG=180��-45��=135�㣮
���AME=��ECF��
���ڡ�AME�͡�ECF�У�
$\left\{\begin{array}{l}{��BAE=��FEC}\\{AM=EC}\\{��AME=��ECF}\end{array}\right.$��
���AME�ա�ECF��
��AE=EF��
��3����AB��ȡһ��M��ʹAM=EC������ME��
��BM=BE��
���BME=45�㣬
���AME=135�㣬
��CF�����ƽ���ߣ�
���DCF=45�㣬
���ECF=135��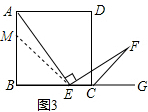
���AME=��ECF
�ߡ�AEB+��BAE=90�㣬��AEB+��CEF=90��
���BAE=��CEF
���ڡ�AME�͡�ECF�У�
$\left\{\begin{array}{l}{��BAE=��FEC}\\{AM=EC}\\{��AME=��ECF}\end{array}\right.$��
���AME�ա�ECF��ASA����
��AE=EF��
���� ���⿼���������ε����ʺ�ȫ�������ε��ж������ʣ�Ҫע����Ŀ֮�����ϵ����ȷ���������߹���ȫ�ȵ��������DZ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
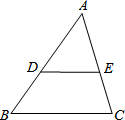 ��ͼ���ڡ�ABC�У�DE��BC��AD=3cm��BD=2cm�����ADE���ABC�����Ʊ�Ϊ$\frac{3}{5}$��
��ͼ���ڡ�ABC�У�DE��BC��AD=3cm��BD=2cm�����ADE���ABC�����Ʊ�Ϊ$\frac{3}{5}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
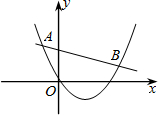 ��ͼ��ʾ����֪���κ���y1=ax2+bx+c��a��0����һ�κ���y2=kx+m��k��0����ͼ���ཻ�ڵ�A��-2��4����B��8��2��������ͼ��ش�
��ͼ��ʾ����֪���κ���y1=ax2+bx+c��a��0����һ�κ���y2=kx+m��k��0����ͼ���ཻ�ڵ�A��-2��4����B��8��2��������ͼ��ش��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
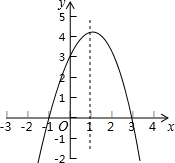 ��ͼ����ֱ������ϵ�У�������y=ax2+2x+c����A��B����y�ύ���C��0��3������PΪ�����߶Գ���x=l��һ���㣮
��ͼ����ֱ������ϵ�У�������y=ax2+2x+c����A��B����y�ύ���C��0��3������PΪ�����߶Գ���x=l��һ���㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
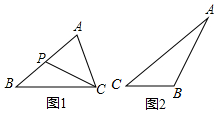 ������ѧϰ����������ʱ���ڱ�������������̿�����꼶�ϲ��31ҳ��������һ���⣬��ͼ1���ڡ�ABC�У�P�DZ�AB�ϵ�һ�㣬����CP��Ҫʹ��ACP�ס�ABC������Ҫ�����һ�������ǡ�ACP=��B�����APC=��ACB������AC2=AP•AB��
������ѧϰ����������ʱ���ڱ�������������̿�����꼶�ϲ��31ҳ��������һ���⣬��ͼ1���ڡ�ABC�У�P�DZ�AB�ϵ�һ�㣬����CP��Ҫʹ��ACP�ס�ABC������Ҫ�����һ�������ǡ�ACP=��B�����APC=��ACB������AC2=AP•AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
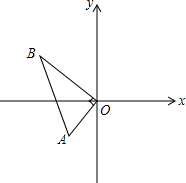 ��ͼ����Rt��AOB�У���AOB=90�㣬��֪��A��-1��-1������B�ڵڶ����ޣ�OB=2$\sqrt{2}$��������y=$\frac{3}{5}$x2+bx+c������A��B��
��ͼ����Rt��AOB�У���AOB=90�㣬��֪��A��-1��-1������B�ڵڶ����ޣ�OB=2$\sqrt{2}$��������y=$\frac{3}{5}$x2+bx+c������A��B���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20��21��29 | B�� | 16��28��34 | C�� | 3��4��5 | D�� | 5��12��13 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com