
 ��ͼ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬B�������Ϊ��3��0������y�ύ�ڵ�C��0��-3������P��ֱ��BC�·��������ϵ�����һ�㣮
��ͼ����ƽ��ֱ������ϵ�У����κ���y=x2+bx+c��ͼ����x�ύ��A��B���㣬B�������Ϊ��3��0������y�ύ�ڵ�C��0��-3������P��ֱ��BC�·��������ϵ�����һ�㣮���� ��1�����ݴ���ϵ�������ɵú�������ʽ��
��2���������εĶԽ����ഹֱƽ�֣��ɵ�P��������꣬�����Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵô𰸣�
��3���������ۣ��ٵ���PCB=90�㣬���ݻ��ഹֱ������ֱ�ߵ�һ����ϵ����Ϊ���������ɵ�BP�Ľ���ʽ�������Ա����뺯��ֵ�Ķ�Ӧ��ϵ���ɵ�P�����ꣻ���ݹ��ɶ������ɵ�BC��CP�ij�����������Ա߶�Ӧ�ɱ����Ҽн���ȵ��������������ƣ��ɵô𰸣�
�ڵ���BPC=90��ʱ���������������ε����ʣ��ɵ�P������꣬��������Ա߶�Ӧ�ɱ����Ҽн���ȵ��������������ƣ��ɵô𰸣�
��� �⣺��1����B��C����뺯������ʽ����
$\left\{\begin{array}{l}{9+3b+c=0}\\{c=-3}\end{array}\right.$��
���$\left\{\begin{array}{l}{b=-2}\\{c=-3}\end{array}\right.$��
������κ���y=x2+bx+c�Ľ���ʽΪy=x2-2x-3��
��2���ı���POP��CΪ���Σ���
OC��PP�以�ഹֱƽ�֣���
yP=$\frac{OC}{2}$-$\frac{3}{2}$����x2-2x-3=-$\frac{3}{2}$��
���x1=$\frac{2+\sqrt{10}}{2}$��x2=$\frac{2-\sqrt{10}}{2}$���ᣩ��P��$\frac{2+\sqrt{10}}{2}$��-$\frac{3}{2}$����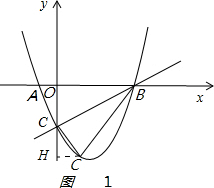 ��3����PBC��90�㣬
��3����PBC��90�㣬
����ͼ1��
����PCB=90��ʱ����P��PH��y���ڵ�H��
BC�Ľ���ʽΪy=x-3��CP�Ľ���ʽΪy=-x-3��
���P��������m��-3-m����
����P�������y�Tx2-2x-3��
���m1=0���ᣩ��m2=1����P��1��-4����
AO=1��OC=3��CB=$\sqrt{{3}^{2}+{3}^{2}}$=3$\sqrt{2}$��CP=$\sqrt{{1}^{2}+��-4+3��^{2}}$=$\sqrt{2}$��
��ʱ$\frac{BC}{OC}$=$\frac{CP}{AO}$=3����AOC�ס�PCB��
����ͼ2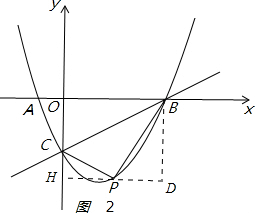 ��
��
����BPC=90��ʱ����PH��y����H����BD��PH��D��
BC�Ľ���ʽΪy=x-3��CP�Ľ���ʽΪy=$\frac{\sqrt{5}-3}{2}$x-3��
���P��������m��m2-2m-3����
��Kcp•Kpb=-1����m=$\frac{1+\sqrt{5}}{2}$��$\frac{1-\sqrt{5}}{2}$����ȥ��
��ʱ��$\frac{PC}{BP}$=$\frac{\sqrt{3}}{\sqrt{15}}$=$\frac{\sqrt{5}}{5}$��$\frac{CO}{AO}$=3��
��P��C��BΪ��������������AOC�����ƣ�
����������P��C��BΪ��������������AOC���ƣ���ʱ��P�����꣨1��-4����
���� ���⿼���˶��κ����ۺ��⣬���ô���ϵ������������ʽ���������ε����ʵó�P��������ǽ���ؼ����������������ε��ж������ʵó�����m�ķ����ǽ���ؼ���


 ��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д�
��˼ά������ҵ��ټ��ִ�ѧ������ϵ�д� �����������Ż�ѧϰϵ�д�
�����������Ż�ѧϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
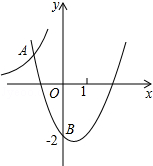 ��ͼ�����κ���y=x2+bx+c��ͼ�����B��0��-2�������뷴��������y=-$\frac{12}{x}$��ͼ���ڵ�A��m��4������������κ����Ľ���ʽ��
��ͼ�����κ���y=x2+bx+c��ͼ�����B��0��-2�������뷴��������y=-$\frac{12}{x}$��ͼ���ڵ�A��m��4������������κ����Ľ���ʽ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ���ڡ�ABC�У���C=90�㣬AC=8cm��BC=6cm��D��б��AB���е㣮��P�ӵ�B������BC���������˶����ٶ�Ϊ1cm/s��ͬʱ����Q�ӵ�A��������AC���������˶����ٶ�Ϊ2cm/s������Qֹͣ�˶�ʱ����PҲֹͣ�˶�������PQ��PD��QD�����˶�ʱ��Ϊt��s����0��t��4����
��֪����ͼ���ڡ�ABC�У���C=90�㣬AC=8cm��BC=6cm��D��б��AB���е㣮��P�ӵ�B������BC���������˶����ٶ�Ϊ1cm/s��ͬʱ����Q�ӵ�A��������AC���������˶����ٶ�Ϊ2cm/s������Qֹͣ�˶�ʱ����PҲֹͣ�˶�������PQ��PD��QD�����˶�ʱ��Ϊt��s����0��t��4�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
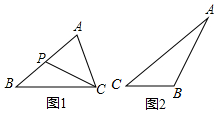 ������ѧϰ����������ʱ���ڱ�������������̿�����꼶�ϲ��31ҳ��������һ���⣬��ͼ1���ڡ�ABC�У�P�DZ�AB�ϵ�һ�㣬����CP��Ҫʹ��ACP�ס�ABC������Ҫ�����һ�������ǡ�ACP=��B�����APC=��ACB������AC2=AP•AB��
������ѧϰ����������ʱ���ڱ�������������̿�����꼶�ϲ��31ҳ��������һ���⣬��ͼ1���ڡ�ABC�У�P�DZ�AB�ϵ�һ�㣬����CP��Ҫʹ��ACP�ס�ABC������Ҫ�����һ�������ǡ�ACP=��B�����APC=��ACB������AC2=AP•AB���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 20��21��29 | B�� | 16��28��34 | C�� | 3��4��5 | D�� | 5��12��13 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | y1��y2��y3 | B�� | y1��y3��y2 | C�� | y3��y1��y2 | D�� | y2��y3��y1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com