
 已知:如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,D是斜边AB的中点.点P从点B出发沿BC方向匀速运动,速度为1cm/s;同时,点Q从点A出发,沿AC方向匀速运动,速度为2cm/s.当点Q停止运动时,点P也停止运动.连接PQ、PD、QD.设运动时间为t(s)(0<t<4).
已知:如图,在△ABC中,∠C=90°,AC=8cm,BC=6cm,D是斜边AB的中点.点P从点B出发沿BC方向匀速运动,速度为1cm/s;同时,点Q从点A出发,沿AC方向匀速运动,速度为2cm/s.当点Q停止运动时,点P也停止运动.连接PQ、PD、QD.设运动时间为t(s)(0<t<4).分析 (1)由等腰直角三角形的性质可知CQ=CP,解得结果;
(2)过Q作QF⊥AB,交AB于,过点P作PE⊥AB,易得Rt△AQF∽Rt△ABC,由相似三角形的性质可得$\frac{QF}{BC}$=$\frac{AF}{AC}$=$\frac{AQ}{AB}$,可得QF,BE,同理可得PE,BE,利用三角形的面积公式可得y与t之间的函数关系式,由△PQD的面积是Rt△ABC的面积的$\frac{1}{4}$,可解得t;
(3)由勾股定理可得QD2,PD2,PQ2,因为PD⊥QD,利用勾股定理可得PQ2=QD2+PD2,解得t.
解答 解:(1)∵△PQC是等腰直角三角形,
∴CQ=CP,
∴8-2t=6-t
t=2 (秒);
(2)过Q作QF⊥AB,交AB于,过点P作PE⊥AB,
∵∠A=∠A,∠AFQ=∠ACB=90°,
∴Rt△AQF∽Rt△ABC,
∴$\frac{QF}{BC}$=$\frac{AF}{AC}$=$\frac{AQ}{AB}$,
∵BC=6,AC=8,AB=10,AQ=2t,
∴QF=$\frac{6}{5}t$,AF=$\frac{8}{5}$t
同理可得:PE=$\frac{4}{5}t$,BE=$\frac{3}{5}t$,
∴y=$\frac{1}{2}×6×8$-$\frac{1}{2}×(6-t)$×(8-2t)-$\frac{1}{2}×5×\frac{6}{5}t$$-\frac{1}{2}×5×\frac{4}{5}t$=-t2+5t;
∵△PQD的面积是Rt△ABC的面积的$\frac{1}{4}$,
∴-t2+5t=6,解得:t1=3,t2=2,
答:当t=3秒或t=2秒时,△PQD的面积是Rt△ABC的面积的$\frac{1}{4}$;
(3)∵${QD}^{2}{=(\frac{6}{5}t)}^{2}{+(5-\frac{8}{5}t)}^{2}$,
同理可得:${PD}^{2}{=(\frac{4}{5}t)}^{2}{+(5-\frac{3}{5}t)}^{2}$,PQ2=(8-2t)2+(6-t)2,
当PD⊥QD时,PQ2=QD2+PD2,
此时,t=$\frac{25}{11}$ (秒),
答:当t=$\frac{25}{11}$时,PD⊥QD.
点评 本题主要考查了相似三角形的性质及判定,等腰三角形的性质和勾股定理等,作出恰当的辅助线利用相似三角形的判定及性质是解答此题的关键.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:填空题
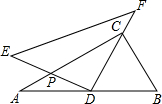 将一副三角尺如图摆放,其中在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中,∠EDF=90°,∠E=45°.点D为边AB的中点,DE交AC于点P,DF经过点C,将△EDF绕点D顺时针方向旋转角α(0°<α<60°)后得△E′DF′,DE′交AC于点M,DF′交BC于点N,那么$\frac{PM}{CN}$的值为$\frac{\sqrt{3}}{3}$.
将一副三角尺如图摆放,其中在Rt△ABC中,∠ACB=90°,∠B=60°,在Rt△EDF中,∠EDF=90°,∠E=45°.点D为边AB的中点,DE交AC于点P,DF经过点C,将△EDF绕点D顺时针方向旋转角α(0°<α<60°)后得△E′DF′,DE′交AC于点M,DF′交BC于点N,那么$\frac{PM}{CN}$的值为$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的任意一点.
如图,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的任意一点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com